Fizzy Clockwork
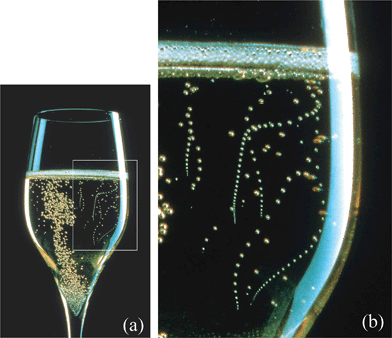
If you pay close attention, you'll find that the bubbles in a glass of champagne form a steady stream and leave the surface of the glass in regular time intervals, . Why is this?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Bubbles grow at the surface of a champagne glass when gas dissolved in the champagne is absorbed into a growing bubble at an imperfection in the glass.
When the bubble is small, the buoyant force pulling it upward is small compared to the adhesive force keeping it stuck to the surface. As the bubble grows, the buoyant force increases linearly in the volume ( ∼ V ), while the adhesive force is proportional to the surface area of the bubbles, or ∼ V 2 / 3 . Clearly, at some point, the buoyant force must overtake the adhesive force, at which point the bubble breaks free from the imperfection in the surface, and rises to the surface.
Assuming deterministic physics, the timing of the initiation of bubble formation, as well as the dynamics of the growth of the bubble should be identical for each bubble, and thus take an identical amount of time from start to finish, thus explaining the constant time intervals between bubble release.