Flat Earth Theory
Suppose there is a solid, uniform circular disk of mass M and radius R . This disk represents a "flat Earth".
A massive point-particle is located a distance R from the plane of the disk along the disk's central axis. What gravitational acceleration does it experience (in m/s 2 )?
Details and Assumptions:
1)
M
=
Earth mass
=
5
.
9
7
2
×
1
0
2
4
kg
2)
R
=
Earth radius
=
6
3
5
6
×
1
0
3
m
3)
Gravity constant
=
6
.
6
7
4
×
1
0
−
1
1
N
m
2
kg
−
2
4)
Give your answer as a positive number
The answer is 5.779.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
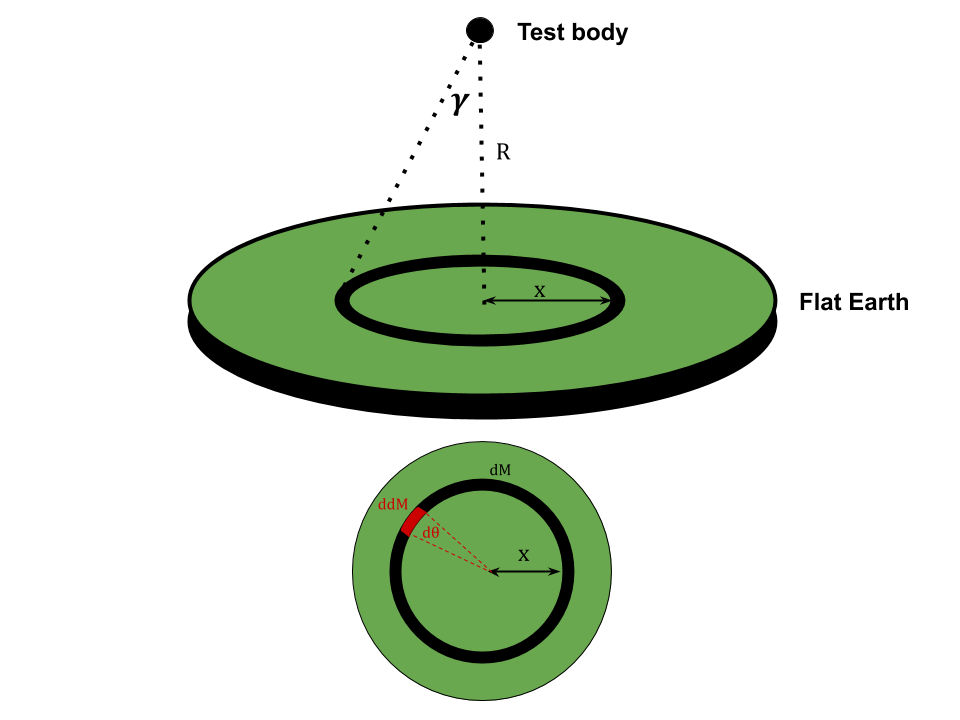 Diagram of flat Earth situation
It is immediately obvious that, due to symmetry, the horizontal component of the gravitational acceleration will be null. To set up the process of solving, we will divide the flat earth into infinitesimally small circular rings of inner radius
x
, mass
d
M
and width
d
x
(with
x
ranging from
0
to
R
). Then, we are going to divide each ring into infinitesimal pieces of mass
d
d
M
, delimiting a central angle
d
θ
. Let us use the following notations:
Γ
– for the strength of the total gravitational field,
d
Γ
– for the strength gravitational field generated by a full ring,
d
d
Γ
– for the strength of the vertical component of gravitational field generated by each piece of a ring. Yikes, enough formalities - let's start integrating!
d
d
Γ
=
R
2
+
x
2
G
d
d
m
cos
γ
=
(
R
2
+
x
2
)
3
/
2
G
R
d
d
m
,
d
d
m
=
2
π
d
m
d
θ
,
d
m
=
π
R
2
2
π
M
x
d
x
d
Γ
=
2
π
(
R
2
+
x
2
)
G
R
d
m
∫
0
2
π
d
θ
⟹
Γ
=
π
R
2
2
π
G
R
M
∫
0
R
(
R
2
+
x
2
)
3
/
2
x
d
x
Γ
=
R
2
G
M
[
∫
2
(
R
2
+
x
2
)
3
/
2
d
(
R
2
+
x
2
)
]
x
=
0
R
=
R
R
2
+
x
2
2
Γ
M
∣
∣
∣
∣
x
=
0
R
∣
Γ
∣
=
R
2
G
M
(
2
−
2
)
⟹
∣
Γ
∣
≈
5
.
7
7
9
m
s
−
2
Diagram of flat Earth situation
It is immediately obvious that, due to symmetry, the horizontal component of the gravitational acceleration will be null. To set up the process of solving, we will divide the flat earth into infinitesimally small circular rings of inner radius
x
, mass
d
M
and width
d
x
(with
x
ranging from
0
to
R
). Then, we are going to divide each ring into infinitesimal pieces of mass
d
d
M
, delimiting a central angle
d
θ
. Let us use the following notations:
Γ
– for the strength of the total gravitational field,
d
Γ
– for the strength gravitational field generated by a full ring,
d
d
Γ
– for the strength of the vertical component of gravitational field generated by each piece of a ring. Yikes, enough formalities - let's start integrating!
d
d
Γ
=
R
2
+
x
2
G
d
d
m
cos
γ
=
(
R
2
+
x
2
)
3
/
2
G
R
d
d
m
,
d
d
m
=
2
π
d
m
d
θ
,
d
m
=
π
R
2
2
π
M
x
d
x
d
Γ
=
2
π
(
R
2
+
x
2
)
G
R
d
m
∫
0
2
π
d
θ
⟹
Γ
=
π
R
2
2
π
G
R
M
∫
0
R
(
R
2
+
x
2
)
3
/
2
x
d
x
Γ
=
R
2
G
M
[
∫
2
(
R
2
+
x
2
)
3
/
2
d
(
R
2
+
x
2
)
]
x
=
0
R
=
R
R
2
+
x
2
2
Γ
M
∣
∣
∣
∣
x
=
0
R
∣
Γ
∣
=
R
2
G
M
(
2
−
2
)
⟹
∣
Γ
∣
≈
5
.
7
7
9
m
s
−
2
@Victor Dumbrava nice solution friend.
With ρ = π R 2 M being the mass density of the disk, the force acting on a particular of mass m is G m ∫ 0 R R 2 + r 2 2 π r ρ R 2 + r 2 R d r = 2 π G m ρ R ∫ 0 R ( R 2 + r 2 ) 2 3 r d r = 2 π G m ρ R [ − R 2 + r 2 1 ] 0 R = 2 π G m π R 2 M R ( R 1 − R 2 1 ) = R 2 G m M ( 2 − 2 ) acting along the central axis of the disk, and hence the acceleration felt by the particle is R 2 G M ( 2 − 2 ) = 5 . 7 7 9 m s − 2 .
The mathematics is very simple, But am having trouble with the initial setup of the integral.
I am assuming from the idea that the point-particle is on the central axis of the circular disk, implies that it is perpendicular to the radius of the disk (Forming a right angle triangle), generating the second multiplication term in the initial setup of the integral, as the distance between the centre of the uniform disk and the point-particle. Alongside the first term, you are taking rings of the disk and summing up each individual circle made from radius 0 to R.
Log in to reply
Imagine a circular ring of radius r and infinitesimal thickness d r inside the main disk. The mass of the ring is 2 π r ρ d r , and every point on this ring is a distance R 2 + r 2 from the test mass. The line from any point on this circle makes an angle θ with the axis of the disk, where cos θ = R 2 + r 2 R . Thus the component of gravitational force along the axis of the disk due to the small ring is G m R 2 + r 2 2 π r ρ d r cos θ and we just add up over all rings, obtaining the integral. By symmetry, the force acting on the test particle is along the axis of symmetry, and so we are done.
Log in to reply
@Mark Hennings thanks for your awesome explanation. You are also legend.