Flatland And Three-Dimensional Shapes
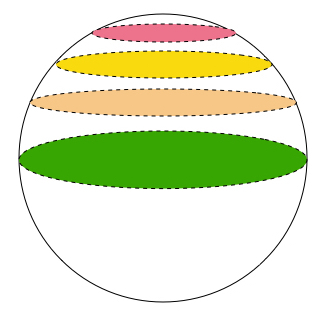
In Flatland, all its inhabitants are confined to a single two-dimensional plane (just like we are confined to a single three-dimensional space). When a sphere passes through the plane, a Flatland inhabitant can only see a circle that gradually grows to a maximum size, before it shrinks again and vanish.
On another occasion, a Flatland inhabitant claims that it saw a triangle that gradually grew, then became a hexagon for a while, then turned back to a triangle and shrunk away. What three-dimensional object could have it seen?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Unfortunately I don't have diagrams because I don't have the necessary programs/abilities to do them well enough. If someone can make animated pictures (or even just some diagrams), it will be appreciated.
Essentially, we have a plane (the plane where Flatland inhabitants live) that's passing through a 3D object, and we observe the cross section changing over time. For example, for a sphere, a plane passing through it will first make contact as a point. Then, as the plane goes further, the cross section becomes a circle that's growing until when the plane divides the sphere in two equal pieces. Then, as the plane continues, the cross section now shrinks, until when it's back to a point and then vanishes.
The problem is that for all six choices, the resulting cross section differs when the plane goes in a different direction. As a simple example, consider a cube A B C D . E F G H . We have several possibilities on the resulting cross section.
- If the plane goes in the direction of an edge, say A E in that direction, the resulting cross section will be a square that suddenly appears (when the plane passes A B C D ), lingers for a while (the vertices of this square are on A E , B F , C G , D H ), and finally vanishes instantly (when the plane passes E F G H ).
- If the plane goes in the direction of a face diagonal, say A C in that direction, the resulting cross section will be a line that suddenly appears (when the plane passes A E ), grows to a rectangle (the vertices are on A B , A D , E H , E F ), reaches a maximum size ( B D H F ), shrinks again down to a line (the vertices are on B C , D C , H G , F G ), and finally vanishes ( C G ).
- If the plane goes in the direction of a space diagonal, say A G in that direction, the resulting cross section will be a point ( A ), growing to a triangle (vertices on A B , A D , A E ), reaches a maximum size ( B D E ), becomes a hexagon for a while (vertices on B C , D C , D H , E H , E F , B F ), finally turns back to a triangle ( C H F ), and shrinks down back to a point ( G ).
As we can observe in that last point, that's exactly what's described, so the answer is cube .
But what about the other options? How can we prove that they cannot make the described result?
We'll first talk about the polyhedrons: tetrahedron, square pyramid, and triangular prism. The trick is to see that the intersection of a face with the plane must form a single line segment. This is because if we extend the face infinitely, we have a plane, and two planes in space intersect on only a single line, not two or more. This means each face provides at most a single line segment, and thus a single edge to whatever polygon is made in the cross section. But the described result claims seeing a hexagon, while these three choices have less than six faces (tetrahedron has 4, the others have 5), so these are all impossible.
For cone and cylinder, since they have a curved face, the above cannot be applied directly. However, the trick is that in most cases, we will have a non-line curve in the cross section, which means the cross section is neither a triangle nor a hexagon.
For the cylinder: Like above, the plane will intersect the two circular bases in at most one line segment each, so we have two line segments. Clearly, they cannot intersect (because the two circular bases don't intersect). Extend the curved surface infinitely. If the plane is not parallel to the axis, the resulting cross section is an ellipse, and the two line segments will just be chords; we will still have a non-line curve, so it's not a polygon. If the plane is parallel to the axis, the resulting cross section is at most two line segments, so together we have four line segments, not enough to make the hexagon.
For the cone: Extend the cone infinitely. Now, we know that the intersection of a plane and a cone is a conic section, and almost all of them have curved sections: a circle, an ellipse, a parabola, a hyperbola. The only ones that don't are the degenerate ones: a point, a line, two intersecting lines. This means we have at most two line segments; adding one from the base gives three, once again not enough for hexagon.
Thus we have ruled out the other five possibilities, and so indeed the answer is cube .
My first thought is that the viewer was looking at a point of the figure since it showed it was a triangle first. which means it had 2 completely different points in terms of x y and z axis so it could have only been a cube or a cylinder though a cylinder doesn't have points
(The graphics are searched from online at http://stackoverflow.com/questions/20387282/compute-the-cross-section-of-a-cube ALL RIGHTS RESERVED TO Yuchen Zhong at stackoverflow.com)
(I DO NOT OWN the graphics)
(Please delete the graphics if it is cited inappropriately)