Function Machine
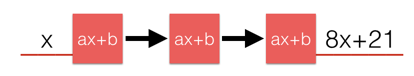 If
f
(
x
)
=
a
x
+
b
, where
a
and
b
are real numbers, and
f
(
f
(
f
(
x
)
)
)
=
8
x
+
2
1
, what is
a
+
b
?
If
f
(
x
)
=
a
x
+
b
, where
a
and
b
are real numbers, and
f
(
f
(
f
(
x
)
)
)
=
8
x
+
2
1
, what is
a
+
b
?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
First we expand the function f ( f ( f ( x ) ) )
We know f ( x ) = a x + b so we can substitute that value in
f ( f ( f ( x ) ) ) = f ( f ( a x + b ) )
From here we expand and simplify
f ( f ( a x + b ) ) = f ( a ( a x + b ) + b )
f ( a ( a x + b ) + b ) = a ( a ( a x + b ) + b ) + b
a ( a ( a x + b ) + b ) + b = a 2 ( a x + b ) + b a + b
a 2 ( a x + b ) + b a + b = a 3 x + b a 2 + b a + b
a 3 x + b a 2 + b a + b = a 3 x + b ( a 2 + a + 1 )
a 3 x + b ( a 2 + a + 1 ) = 8 x + 2 1
Next we separate the x from both equations and put it in one of it's own.
a 3 x = 8 x
b ( a 2 + a + 1 ) = 2 1
Next we simplify the first equation
a 3 = 8
a = 3 8
a = 2
We then substitute that into the other equation
b ( ( 2 ) 2 + ( 2 ) + 1 ) = 2 1
7 b = 2 1
b = 7 2 1
b = 3
Now that we know a and b we can calculate a + b
a + b = ( 2 ) + ( 3 ) = 5
a + b = 5
Nice explanation ,that's exactly how I solved it
Me too but I thought 3+2 was 11 how stupid
it's a + b = 5. duh!
First, find what a x + b is when f ( x ) becomes f ( f ( f ( x ) ) ) . f ( f ( f ( x ) ) ) = a ( a ( a x + b ) + b ) + b f ( f ( f ( x ) ) ) = a 3 x + a 2 b + a b + b Since x only appears once in the equation, we can determine from the given function, f ( f ( f ( x ) ) ) = 8 x + 2 1 , that a 3 = 8 . Hence, a = 2 . If you plug a back into the most recent function, you get f ( f ( f ( x ) ) ) = 8 x + 4 b + 2 b + b = 8 x + 7 b Looking back at the given function, we can determine that 7 b = 2 1 ⟹ b = 3 Therefore, a + b = 5 .