Flipping 3 Coins
There are 10 coins, 5 of which are heads up and 5 of which are tails up.
On each turn, you choose exactly 3 coins and flip them over.
What is the minimum number of turns needed to make all of the coins heads up?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
A quicker way of showing that 2 is not possible, is to count the parity of the number of heads. This changes each turn, so the number of turns we need must be odd.
Log in to reply
That is very nice. Thanks!
Log in to reply
Could you update the solution?
We can also generalize it to the game of having N coins, T tails, and flip C coins each turn.
sorry I don't know where to post this, but why when solving a problem in problems of the week requires me to solve it again when I click on a notification? and is solving it incorrectly the second time will drop my level?
It is easy to overlook you MUST flip 3 coins each turn.
What if we choose three tails, and after flipping over we get again three tails. Nothing can guarantee that it can be changed even after three or more turns! A posteriori knowledge is of no help in this regard! On the other hand, after flipping first time, three tails can make three heads up, and in the next turn, the remaining two tails can also make two heads up whereby one head remain head, That's how we can have only two turns! So, the question posed in this sense is apsurd!
Although this solution is completely correct, this approach isn't well suited to handle other variations of this problems (e.g. if the numbers were larger). Alternatively, consider arranging the numbers 0 through 10 in sequential order into three columns. These numbers will represent the numbers of heads we see. Add connections to adjacent numbers (either horizontal or vertical) to represent that the possible changes that can be done in the game. The question now becomes, "What is the shortest path from 5 to 10?" Thinking of taxicab (grid-like) distance, it is clear that this is 3.
Remember that to prove something is a minimum, we have to show that
1) It can be achieved,
2) No smaller number can be achieved.
Most solutions here only shown that 3 can be achieved, so I will skip that. Instead, I will focus on showing that "No smaller number can be achieved". Since we need to flip over 5 coins, it is clear that
1
<
3
5
cannot be achieved. However, can 2 be achieved? Is there a way to magically flip 6 coins so that they all end up heads?
In this approach, we use the invariant principle , where the idea is to find something that "stays fixed". For a given configuration on turn t , define "N_t = Number of heads - number of tails". For example, we start off with N 0 = 5 − 5 = 0 , and want to reach N = 1 0 − 0 = 1 0 .
Let's consider how this number changes:
If we flip a head to a tail, we will change:
N
t
+
1
−
N
t
=
−
1
−
1
=
−
2
.
If we flip a tail to a head, we will change:
N
t
+
1
−
N
t
=
+
1
+
1
=
+
2
.
Ah, so that's a start! When we flip 3 coins, we thus change
N
by
−
2
−
2
−
2
=
−
6
,
−
2
−
2
+
2
=
−
2
,
−
2
+
2
+
2
=
2
,
+
2
+
2
+
2
=
6
. Now, another way to rephrase the question is: What is the minimum number of turns to go from 0 to 10, where we can only use
−
6
,
−
2
,
+
2
,
+
6
each turn?
If we divide out the numbers by 2, the question becomes:
What is the minimum number of turns to go from 0 to 5, where we can only use − 3 , − 1 , + 1 , + 3 each turn?
Now, it is clear that each turn we use one of − 3 , − 1 , + 1 , + 3 , we are changing the parity of N t . Since N t goes from an odd to even number, hence we can conclude that the number of turns used must be odd! Thus, from here, we can show that N = 2 cannot be achieved!
Note: The reason that I "divide out the number by 2", is to make the parity argument clearer. We could have looked at the values mod 4, and see how it changed.
Note: To keep to the invariance principle spirit of "something that stays fixed", we could say that the parity of
N
t
−
t
is always even. Hence, when
t
=
2
, we cannot get
N
2
=
5
.
In general, once you found the underlying pattern (as we did above), you're set.
Generalization
Using the above approach, consider the case of
S
starting coins with
H
heads and we can flip
F
coins each turn. When is this possible?
If it is possible, how many turns do we need?
Can you find a specific case where this is not possible?
I love your challenge for general case. Came across it when interviewing for the school scholarship)
Start : Step 1 : Step 2 : Step 3 : ⊕ ⊕ ⊕ ⊕ ⊕ ⊕ ⊕ ⊕ ⊕ ⊕ ⊕ ⊕ ⊕ ⊕ ⊖ ⊕ ⊕ ⊕ ⊖ ⊕ ⊖ ⊖ ⊖ ⊕ ⊖ ⊖ ⊕ ⊕ ⊖ ⊕ ⊕ ⊕ ⊖ ⊕ ⊕ ⊕ ⊖ ⊕ ⊕ ⊕
Note: ⊕ denotes head. ⊖ denotes tail.
In response to Nicolas Bryenton 's comments , we note that there are 5 coins to be flipped and since each turn we can only flip 3 coins, we need more than 2 turns to complete the task. Since 3 is the smallest integer greater than 2, the minimum number of turns is therefore 3 .
All you have done is shown that the game can be completed with three turns. You have not shown that this number is minimum.
Log in to reply
Indeed! That's one of my pet peeves :)
I have replied.
can we generalize it?
Log in to reply
Yes, starting with n heads and n tails. Then the minimum number of turns is given by:
t min = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ 3 n ⌊ 3 n ⌋ + 3 ⌊ 3 n ⌋ + 2 if n m o d 3 = 0 if n m o d 3 = 1 if n m o d 3 = 2
We have , number of heads up coins H n = 5 and number of tails up coins T n = 5 Since we are provided to flip 3coins at a time and target is to arrange all coins into heads up with minimum turns. To complete the task, the tails up coin should be formed in the multiple of 3. (as 3 flips at a time).Since 5 coins are already in tails up position and it nearest multiple of 3 is 6. H H H H H T T T T T step 1 : Getting tails up coins from 5 to 6 by flipping two heads up into tails and one tails up into head as H H H T T H T T T T
Step 2 : Flipping 3 tails up coins without altering heads up coins as H H H H H H T T T
Step3 : Finally fliping left 3 tails up coins and all 10 coins are heads up . H H H H H H H H H H Hence minimum turns are 3 .
Reminder: To show that something is a minimum, we have to show that 1) It can be attained, and 2) No smaller number will work.
You have done 1), but not 2).
Log in to reply
Btw FYI: pix is "wrong"= shows 6/4, not (stated): 5/5..... Thnx d
I thought of it as "how can we make it so that we get 7 heads, so that the next turn we can get a perfect 10?" But I then realized that it would require a lot of turns. So then I asked "how can we make it so that we can get 4 heads so that in 2 turns we can get a perfect 10?", and that seemed to work out easily.
We solve by using a monoinvariant .
First, we consider this table.
| Type | Configuration of 3 coins | After flipping | No. of heads increase/decrease |
| 1 | TTT | HHH | + 3 |
| 2 | TT H | HH T | + 1 |
| 3 | T HH | H TT | − 1 |
| 4 | HHH | TTT | − 3 |
So, after each turn, the parity of the number of coins which heads up changes.
At the begin, the number of coins which heads up is 5 , hence, the number of coins which heads up can be 1 0 after an odd number of steps.
We note that we cannot make all of the coins heads up after 1 turn.
And, we have + 5 = ( + 1 ) + ( + 1 ) + ( + 3 ) , so we can make all of the coins heads up after 3 turns as below:
| Initial | H | H | H | H | H | T | T | T | T | T |
| Turn 1 | H | H | H | H | T | H | H | T | T | T |
| Turn 2 | H | H | H | H | T | H | T | H | H | T |
| Turn 3 | H | H | H | H | H | H | H | H | H | H |
So, the correct answer is 3 .
Let 0 ≤ n ≤ 5 be the number of the least common face (head or tail).
We can flip three of the same kind, increasing or decreasing n by three; or we can flip two of the same kind, one of the opposite kind, increasing or decreasing n by one.
Our goal is to go from n = 5 to n = 0 . Since n always increases or decreases by an odd number, we need an odd number of flips. Since ⌈ Δ n / 3 ⌉ = 2 , we need at least two flips. Therefore the solution must be n = 3 .
There are three different ways to accomplish this, but each involves once flipping over three tails, and twice flipping over two tails and one head.
As others have shown (eg. Chew-Seong Cheong), you can also flip one-tail-and-two-heads once and then flip three-tails twice. Also, I think the last step must be to flip three-tails (a '+3' step below).
1 + 1 + 3 = 5 (in only this order)
-1 + 3 + 3 = 5 (in two orders)
Suppose T is tail and head is H
H H H H H T T T T T
1 ) H H H T T H T T T T
2 ) H H H T T T H H H H
3 ) H H H H H H H H H H
Hence the answer is 3
One head represents +1, one tails represents -1. h is the number of tails flipped on a single turn, and t is the number of heads flipped. The value of pile p(n) is p(n -1)+h -t, where h+t=3. and -5<=p( n )<=5. Since h+t is an odd number,h -t is also an odd number. p( 0 )=5 -5=0 ( even ), and since we want to get to p( x )=5, x must be an odd number ( otherwise you've added an odd number an even number of times, and therefore have an even number ). You can't do it in one turn since there are more than 3 tails. You can't do it in two turns since x=2 is an even number. It works in three turns by: p( 1 )=0 -1, p( 2 )=0 -1+3, p( 3 )=0 -1+3+3. Since 1 and 2 turn are impossible, three is the lowest number of turns as demonstrated.
3 t u r n s :
S t e p 0 : H H H H H T T T T T
S t e p 1 : H H H T T H T T T T
S t e p 2 : H H H H H H H T T T
S t e p 3 : H H H H H H H H H H
It is obvious that you can’t do it in one turn, for you can only have 8 heads at maximum.
You also cannot do it in two turns: you are flipping 3 coins each turn, so after any odd-number turns you have an even-number of heads, and after any even-number turns you have an odd-number of heads. You can never have 1 0 heads after two turns.
I'm not a "mathy" sort, so I'll explain in my wordy, descriptive language. First, I noticed that since the flips had to be in a set of 3's and I started out with 5 tails up, I realized that I needed to get the 5 to a number divisible by 3 by flipping a Heads to a Tails from the get-go. So, flipping 2 Heads and one Tails on my first flip now gives me 6 Tails which I can now flip in 3's on 2 additional turns. Viola'! Three turns and all Heads up.
There are 5 heads (H) and 5 tails (T). At the last turn 3 last tails may be flipped to Heads. In one turn it is impossible to convert 5 tails into 3 tails without flipping one head to tail. So the strategy will be be Step 1 - HTT -->THH (Total 4 tails) Step 2 HTT -->THH (total 3 tails) Step 3 TTT --->HHH (total 0 tails)
10 = 1(mod)3. 5=2(mod3) ergo (10-5) = 2 (mod 3). Therefore flipping 3 of the same coin will still be 2( mod 3). As we have to flip three coins every time, we have to increase the number of heads by+/-1 or 3. As 3 has no effect we need +/-1. Which makes the difference 1 (mod3) in either case. On the second iteration flipping the opposite sign just leads to an infinite loop, so we flip the same sign, leading to 0 ( mod3) in 2 steps. From there we just need to flip 3 of the same until the goal of uniformity is reached ( in this case once) for a net total of three flips.
It is obviously not possible to achieve the objective with one turn, since the number of coins which need to become heads is more than 3 (5 to be precise).
Before any flips you have 5 Tails & 5 Heads After one turn you will either have 2 Tails & 8 Heads (If all 3 flipped coins WERE tails) or STRICTLY MORE THAN 3 tails eg if you flipped 3 coins that WERE 2 tails & 1 Head you would get WITH THESE 1 tail & 2 heads, i.e. you would have only arrived at ONE LESS TAIL, so you would have 4 tails. And before the final turn you need EXACTLY 3 TAILS. So that you can flip all these and arrive with all coins are heads. And 3 tails is imposible to achieve after 1 flip. I hope that I've shown this to your satisfaction.
For 3 turns, if in the first turn you flip 2 tails & 1 head, you would arrive at 1 tail & 2 heads which would be a NETT INCREASE of one head. Repeat that process to have an additional nett increase of 1 head. And then you would have 7 heads and 3 tails, a nett increase of 2 heads in the first two turns. And then you would have your 3 tails that you required to be able to flip all these on the 3rd turn to arrive at 10 heads with no tails at all - the outcome that you were aiming for.
This has been quite a difficult problem to expain, and I hope that I've succeeded for you?
Regards, David
Possible effects of one turn (need to be careful not to turn coins that aren't there):
| Turn 3 tails | +3 heads |
| Turn 2 tails, 1 head | +1 head |
| Turn 1 tail, 2 heads | -1 head |
| Turn 3 heads | -3 heads |
On turn 1:
- From 5 heads, can get to 2,4,6 or 8 heads
on turn 2
- From 8 heads, can get to 7 or 9 heads (also 5 heads, but that would be going backwards - backwards moves ignored after this)
- From 6 heads, can get to 3, 7 or 9 heads
- From 4 heads, can get to 1,3 or 7 heads
- From 2 heads, can get to 1 or 3 heads
on turn 3
- From 9 heads, can't get anywhere new (can't get to ten heads, because that would require turning two tails, that aren't there)
- From 7 heads, can get 10 heads
- From 3 heads, can get 0 heads
- From 1 head, can't get anywhere new
So it takes a minimum of three turns, and, as a bonus, the last turn will always be turning over three tails
I'm not going to be too fancy in my solution, I'm simply stating the sequence that I did with 3 turns :
...
before manipulation:
HHH THTT THT
turn 1: (flip entire bottom row, aka flip 2 tails and 1 head)
HHH THTT HTH
turn 2: (flip 2 different tails and 1 different head)
HHH TTHH HTH
Note that the objective of the first two turns is to set it up such that there are exactly 3 tails to be flipped on the last turn.
turn 3: (flip the remaining 3 tails)
HHH HHHH HHH
note:
•Counterintuitively, the objective is not to flip the most tails per turn. This will not get it done faster.
•Coins that have already been flipped once may be flipped again.
•By my logic, since it is impossible that within 1 or 2 turns, that the last turn would be flipping 3 tails... then 3 turns is the minimum number of turns to achieve all heads.
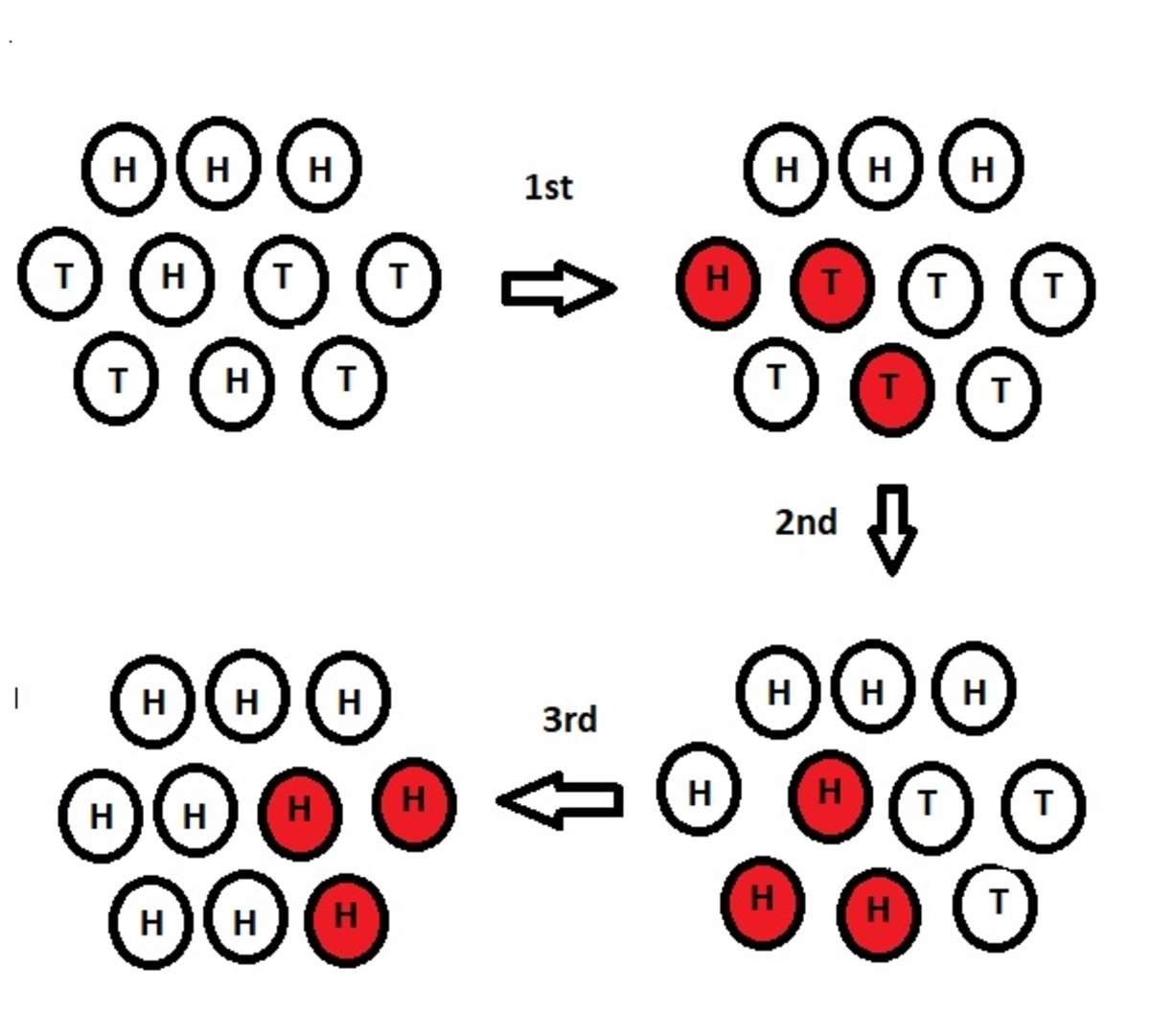
It is trivially impossible to complete the game with one turn. I prove it is impossible with 2.
On the first turn, if three of the tails do not get flipped (i.e., 2 or fewer are flipped), then by the pigeon hole principle, at least one of the heads is flipped. But then, it is impossible to finish the game after one more turn, as the three untouched tails must still be flipped, as well as the tail that was gained on the first turn.
So we may assume that at least three of the tails are turned on the first turn. Since only three coins may be flipped per turn, this means exactly three are turned. So, after the first turn, there are exactly 2 tails remaining. It is clear that the game can not be completed with an additional turn, as at least one head must be turned over, by the pigeon hole principle.
Therefore it is impossible to complete the game with 2 turns. I exhibit a sequence of moves that completes the game after 3 moves.
T T T T T H H H H H
H H T T T T H H H H
H H H T T H T H H H
H H H H H H H H H H
So we may conclude that the minimum number of turns required is in fact 3.