Flipping Fractions

Since $\infty=\infty-1$ , $t_{\infty}=t_{\infty-1}$ . Therefore, our equation changes to $t_{\infty}=\frac{1}{1+t_{\infty}}$ .

We can now solve for $t_{\infty}$ .

${t_{\infty}}^2+t_{\infty}-1=0$ .

$t_{\infty}=\frac{\sqrt5-1}{2}$ .

$5+1+2=\boxed8$ .

$\begin{aligned} t_1 & = \frac 1{1+t_0} \\ t_2 & = \frac 1{1+t_1} = \frac 1{1+\frac 1{1+t_0}} \\ t_3 & = \frac 1{1+\frac 1{1+\frac 1{1+t_0}}} \\ \cdots & = \cdots \end{aligned}$

$\begin{aligned} \implies \lim_{n \to \infty} t_n & = \frac 1{1+\frac 1{1+\frac 1{1+\frac 1{1+\cdots}}}} & \small \color{#3D99F6} \text{Let }\lim_{n \to \infty} t_n = x \\ x & = \frac 1{1+x} \\ x^2 + x - 1 & = 0 \\ \implies x & = \frac {-1+\sqrt {1+4}}2 = \frac {\sqrt 5-1}2 & \small \color{#3D99F6} \text{Since }x > 0 \end{aligned}$

Therefore, $a+b+c = 5+1+2 = \boxed 8$ .

Let $t_m = \frac{p}{q}$ for some positive integers $m$ , $p$ , and $q$ . Then according to the definition of the sequence, $t_{m + 1} = \frac{1}{1 + \frac{p}{q}} = \frac{q}{p + q}$ , and $t_{m + 2} = \frac{1}{1 + \frac{q}{p + q}} = \frac{p + q}{p + 2q}$ , so that:

$\dots, \frac{p}{q}, \frac{q}{p + q}, \frac{p + q}{p + 2q}, \dots$

Let $G$ be a sequence such that $G_{n + 2} = G_n + G_{n + 1}$ , and let $G_n = p$ and $G_{n + 1} = q$ . Then the above sequence becomes:

$\dots, \frac{G_n}{G_{n + 1}}, \frac{G_{n + 1}}{G_{n + 2}}, \frac{G_{n + 2}}{G_{n + 3}}, \dots$

Since $G_n$ and $G_{n + 1}$ are positive, and $G_{n + 2} = G_n + G_{n + 1}$ , $\displaystyle \lim_{n\to\infty} \frac{G_n}{G_{n + 1}}$ converges.

Let $u = \displaystyle \lim_{n\to\infty} a_n = \displaystyle \lim_{n\to\infty} \frac{G_n}{G_{n + 1}} = \displaystyle \lim_{n\to\infty} \frac{G_{n + 1}}{G_{n + 2}}$ . Then $G_{n + 2} = G_n + G_{n + 1}$ becomes $\frac{G_{n + 2}}{G_{n + 1}} = \frac{G_n}{G_{n + 1}} + \frac{G_{n + 1}}{G_{n + 1}}$ , which becomes $\frac{1}{\frac{G_{n + 1}}{G_{n + 2}}} = \frac{G_n}{G_{n + 1}} + 1$ , which becomes $\frac{1}{u} = u + 1$ , which solves to $u = \displaystyle \lim_{n\to\infty} a_n = \frac{\sqrt{5} - 1}{2}$ , so that $a = 5$ , $b = 1$ , $c = 2$ , and $a + b + c = \boxed{8}$ .

---

Note that if $t_0 = 1$ instead, the sequence becomes $1, \frac{1}{2}, \frac{2}{3}, \frac{3}{5}, \frac{5}{8}, \dots$ , which contain numbers in the Fibonacci sequence, and $\displaystyle \lim_{n\to\infty} \frac{F_n}{F_{n + 1}}$ is also equal to $\frac{\sqrt{5} - 1}{2}$ .

Let $y = f(x) = \frac{1}{1+x}$ be a function and $x = t_0 = 10$ be the starting point

Then $t_1 = y = \frac{1}{1 + x} = \frac{1}{1 + 10} = \frac{1}{11}$ , Now to calculate the next term $t_2$ our new input is $x = \frac{1}{11}$ which can be obtained by projecting point $(10 , \frac{1}{11})$ on line $y = x$ and going in this manner we can see that our final value coincides with the intersection of curve $y = \frac{1}{1+x}$ and line $y = x$ i.e. 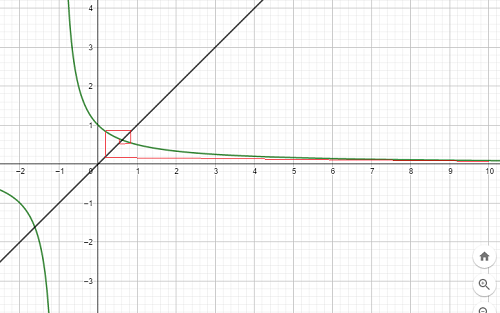$\frac{1}{1+x} = x$

$x^2 + x - 1 = 0$

$x = \frac{\sqrt5 - 1}{2}$

which implies , a = 5 , b = 1 ,c = 2 i.e. $a + b + c = 8$