Flipping Out
In front of you are two coins. They are identical in appearance, but one is fair (when flipped, it comes up Heads 50% of the time), while the other comes up Heads 75% of the time. Your task is to determine which one is the unfair coin.
You will only be permitted two flips total. After you choose your first coin and flip it, you can base your decision of which coin to flip second on your results of the first flip. After you perform your second flip, you will be asked to declare which coin you believe to be the fake.
If you always act so as to maximize the likelihood of your eventually correctly identifying the fake coin, what is the probability that you will correctly identify the fake coin?
If the desired probability is written as n m , where m and n are positive coprime integers, then enter m + n as your answer.
The answer is 53.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
You haven't proven that your strategy is optimal. I'm sure there are simple variants of the question where it wouldn't be.
I don't get it... can someone please explain why my calculations yield 23/32 instead of 21/32? I'm doing it this way:
You flip your first coin (1/2 chance it is biased), giving heads with prob. 5/8 and tails with prob. 3/8.
First case: heads. There's a 3/5 chance the coin is biased.
-
If you keep it, you'll get heads with 3/5×3/4 + 2/5×1/2 = 13/20 chance, and the prob. it is biased is 9/13 (note that the first numerator cancels the second denominator) or you'll get heads with 7/20 chance, and the prob. it is biased is 3/7. The probability of guessing correctly the biased coin is then 13/20×9/13+7/20×4/7 = 13/20 (if the probability that the first coin is biased is 3/7, the probability that the other is biased is 4/7, hence better guess the second is biased).
-
If you change for the other coin, you'll get heads with 12/20 chance, and the prob. the first coin is biased is 1/2 (normal as two different coins giving the same result are undistinguishable) or you'll get heads with 7/20 chance, and the prob. the first coin is biased is 3/4. The probability of guessing correctly the biased coin is then 12/20×1/2+8/20×3/4 = 12/20. Therefore, better keep flipping the same coin, as you'll have a greater chance of guessing which one is biased.
Second case: tails. There's a 1/3 chance the coin is biased. Doing calculations of the same kind, if you keep the coin you'll get 8/12 chance of guessing correctly, if you change, you'll get 5/6 chance, which is better.
Therefore, globally, you'll have 5/8×13/20 + 3/8×5/6 = 23/32 chance of guessing correctly which coin is biased.
I think where I got it wrong is when you make your second flip, the probabilities of your first flip change. But I struggle to find the new probabilities.
Let C1: Normal and C2: Fake, with a preferred convention taken,
C1 C1: (0.5 H1 + 0.5 T1) (0.5 H1 + 0.5 T1) = 0.25 H1 H1 + [0.25 H1 T1] + 0.25 T1 H1 + 0.25 T1 T1
C2 C2: (0.75 H2 + 0.25 T2) (0.75 H2 + 0.25 T2) = [0.5625 H2 H2] + 0.1875 H2 T2 + 0.1875 T2 H2 + 0.0625 T2 T2
C1 C2: (0.5 T1 + 0.5 H1) (0.25 T2 + 0.75 H2) = 0.125 T1 T2 + [0.375 T1 H2] + 0.125 H1 T2 + 0.375 H1 H2
C2 C1: (0.25 T2 + 0.75 H2) (0.5 T1 + 0.5 H1) = [0.125 T2 T1] + 0.125 T2 H1 + 0.375 H2 T1 + 0.375 H2 H1
Since we are actually blind between 1 and 2, we are actually looking for a set of HH, HT, TH and TT. We found a replacement of (0.25 HH + 0.25 HT + 0.25 TH + 0.25 TT) with (0.5625 H2 H2 + 0.25 H1 T1 + 0.375 T1 H1 + 0.125 T2 T1) being available, with extra 0.3125. Chance of getting the right guess when C2 is very close to C1 will be 0.5 where the probability formed will be (0.25 + 0.25 + 0.25 + 0.25)/(0.5 + 0.5 + 0.5 +0.5) = 2 (0.25 + 0.25 + 0.25 + 0.25)/(1 x 4) = 1/ 2. Therefore, the probability wanted should be (0.5625 + 0. 25 + 0.375 + 0.125)/ 2 = 1.3125/ 2 = 0.65625 = 21/ 32.
Method to achieve this maximized probability when the first toss is:
H: Retain for second toss; if same as H, then this is fake suspected; otherwise if different as T, then the first is fake suspected.
T: Toss another coin; if different as H, then this is fake suspected; otherwise if same as T, then the first is fake suspected.
0.5625 H2 H2 + 0.25 H1 T1 + 0.375 T1 H1 + 0.125 T2 T1 tells C1 and C2 by number 1 or number 2. The increased in chance arise from the first toss being H, otherwise, maximizing chance remained would be available from toss of different coins. We are extracting higher distribution of chance along each and every sum of 1 among the 4 types. The change for first toss being T replaced 0.4375 with 0.5, while keeping unchanged for first toss being H replaced 0.75 with 0.8125. Consequently, we have 65.625% of correct guess instead of 50%. Further, this percentage can arrive up to 87.5% when 75% becomes 100%.
Method we use makes the second coin to be wanted fake coin whenever it appears as H, otherwise another one. One must be careful that this is still a chance only but not guaranteed. Nevertheless, we maximized chance of correct guess.
21 + 32 = 53
The biased coin is more likely to land up heads. So, for the first flip, pick one coin at random and flip it. If it comes up heads, use the same coin for your second flip; otherwise, use the other coin. This maximizes the probability that the second coin flipped is the biased coin.
If the second flip comes up heads, declare the coin you last flipped as the biased coin. Otherwise, declare the other coin as the biased coin.
This strategy yields a pretty simple decision tree, shown below. We simply add the probabilities to get 21/32.
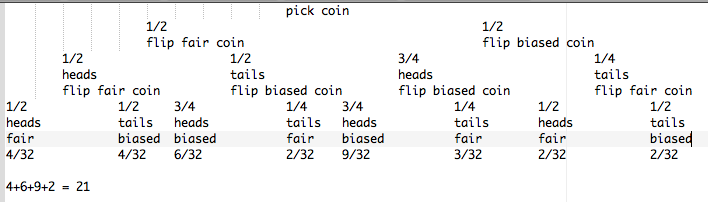
A more rigorous solution is welcome :)
P ( c o r r e c t ) = P ( c o r r e c t ∣ U ) × P ( U ) + P ( c o r r e c t ∣ F ) × P ( F ) For the strategy toss the first choice twice and decide unfair U only if the result is HH we obtain P ( c o r r e c t ) = P ( H H ∣ U ) × P ( U ) + ( P ( H T ∣ F ) + P ( T H ∣ F ) + P ( T T ∣ F ) ) × P ( F ) giving P ( c o r r e c t ) = ( 4 3 ) 2 × 2 1 + ( 4 1 + 4 1 + 1 4 1 ) × 2 1 = 3 2 2 1
Note that it isn't actually better OR worse to flip the other coin if the first one comes up heads. By coincidence, if the first flip is a tails, your guess after your next flip will be accurate 2/3 of the time regardless of whether you switched coins.
We have two coins and we know one is biased and one is fair, this means that if we find out what the type of one coin is, then we can deduce what the other is. For example, if we flip the same coin twice and get Tails, Tails, then it means the coin we picked is likely the fair one and that the other coin will be the biased (fake) one.
Therefore we can simply flip the same coin twice and make our decision based on the outcomes, we will note Heads with H and Tails with T for brevity.
The four possible outcomes of flipping the coin are: HH, HT, TH, TT Now again we use our intuition: if we get HH, then we probably have the biased coin, otherwise, it's more likely we picked the fair coin. Therefore, if we get HH we will say the coin we picked is fake and if we get HT, TH or TT then we will say "this coin is fair, therefore the other coin is fake".
So what are the probabilities? If we picked the fake coin then they are as follows: HH: 3/4 * 3/4 = 9/16 HT: 3/4 * 1/4 = 3/16 TH: 1/4 * 3/4 = 3/16 TT: 1/4 * 1/4 = 1/16
If we picked the fair coin then the probabilities are: HH: 1/2 * 1/4 = 1/4 = 4/16 HT: 1/2 * 1/4 = 1/4 = 4/16 TH: 1/2 * 1/4 = 1/4 = 4/16 TT: 1/2 * 1/4 = 1/4 = 4/16
So when will we pick the correct answer?
If the coin is fake then we will be correct only if it lands HH which is 9/16 of the time, if the coin is fair then we'll be correct in 3 out of the 4 cases, which is 12/16.
BUT! we must take into account we will get the fake coin just 1/2 of the time, therefore we have (9/16 * 1/2) + (12/16 * 1/2) which is 21/32.