Floor+fractional parts

$\begin{aligned} I & = \int_0^4 \{ x \} \lfloor x \rfloor \, dx \\ & = \sum_{k=0}^3 \int_k^{k+1} (x - k)k \, dx \\ & = \sum_{k=0}^3 \left[ \frac{kx^2}{2} - k^2x \right]_k^{k+1} \\ & = \sum_{k=0}^3 \left( \frac{k(2k+1)}{2} - k^2 \right) \\ & = \sum_{k=0}^3 \frac{k}{2} = \frac{1}{2} \sum_{k=1}^3 k = \frac {3 \cdot{} 4}{2 \cdot{} 2} = \boxed{3} \end{aligned}$

the integral above equals

$\displaystyle\int _{ 0 }^{ 4 }{ x\left\lfloor x \right\rfloor dx } -\displaystyle\int _{ 0 }^{ 4 }{ \left\lfloor x \right\rfloor ^{ 2 }dx }$ we break the first integral into multiple parts,namely,

$\displaystyle\int _{ 0 }^{ 1 }{ 0dx } +\displaystyle\int _{ 1 }^{ 2 }{ x } +\displaystyle\int _{ 2 }^{ 3 }{ 2xdx } +\displaystyle\int _{ 3 }^{ 4 }{ 3xdx }$

and the second integral is the sum of squares of the natural numbers from 0 to 3

making our answer $\boxed{3}$

This question becomes relatively straightforward if we consider the integration as the area under the graph. The graph for $y= \{ x \}$ is like a sawtooth wave, and the graph for $y=\left\lfloor x \right\rfloor$ is like a staircase - multiplying these together gives a graph with the following shape: 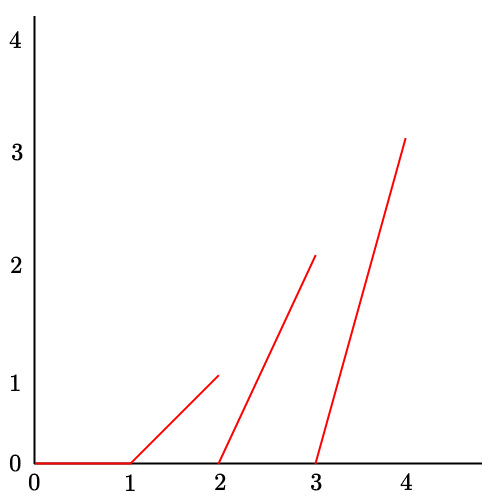The integral is simply the area of the three triangles formed. $\int_0^4 \{ x \} \lfloor x \rfloor \, dx = \dfrac{1}{2}+1+\dfrac{3}{2}=\large \color{#20A900}{\boxed{3}}.$

Break them in the intervals of 1 unit and the floor function would reduce to integer and in 1 interval integration of fractional part is always 0.5 hence the answer is $( 1 + 2 + 3 ) × 0.5 = \boxed{3}$