Flow Rate Problem
Water is poured into a conical tank at the rate of 2.15 cubic meters per minute. The tank is 8 meters in diameter across the top and 10 meters high. How fast the water level rising (in m/min), when the water stands 3.5 meters deep to four decimal places.
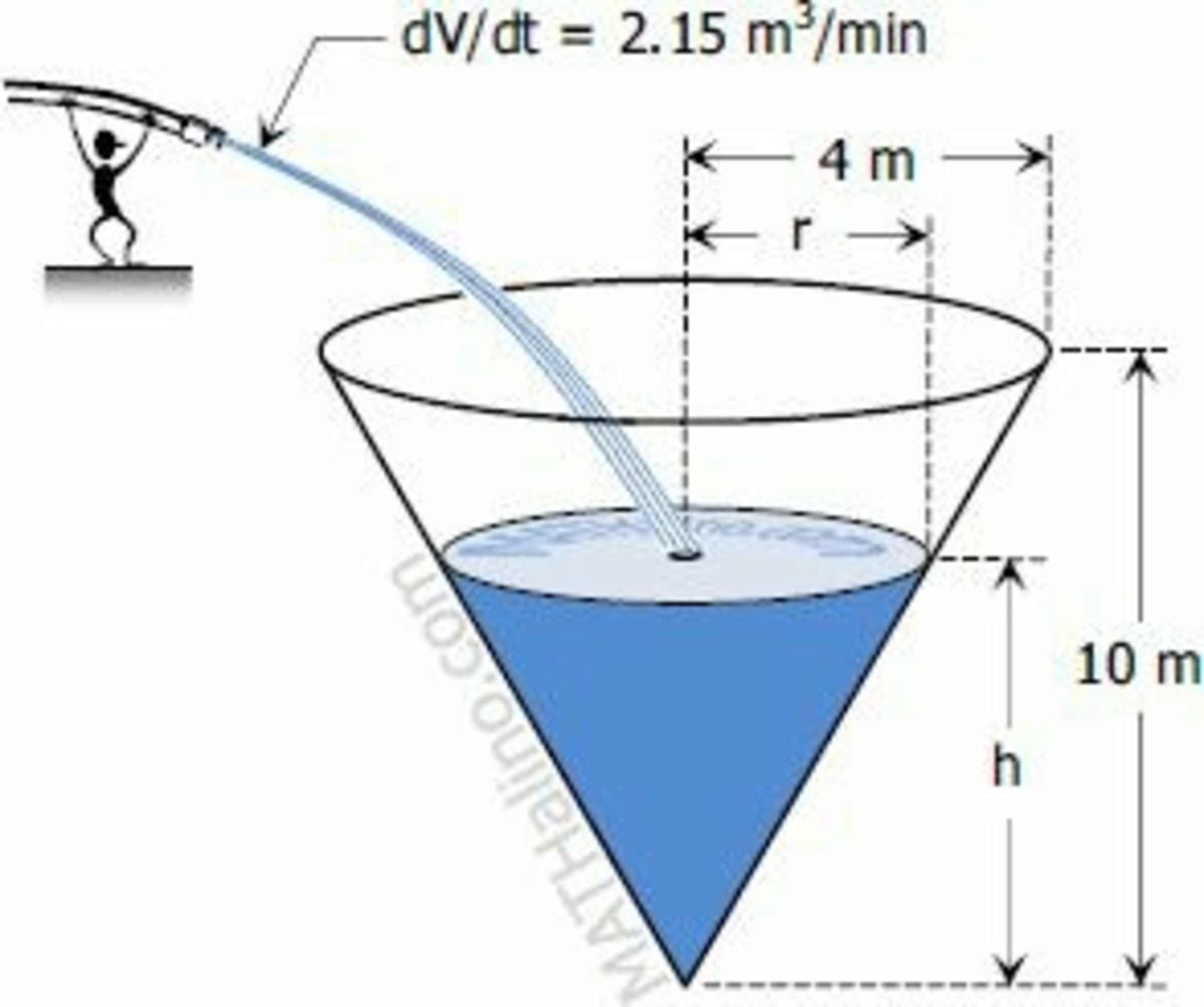
The answer is 0.3492.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Log in to reply
Good to know hahahahaha, I don't know much about applying Calculus to real-life problems, so I'm not quite sure if I'm setting up correct equations. Actually, at first, I thought dt/dh was the one being asked. hahahahaha
Log in to reply
thanks Mr. manuel
you are good in calculus
after all every one has to start the journey and at the end of the day you will reach your destination and get a good answer.
thanks.
The volume of water in the conical tank is given by:
V d t d V ⟹ d t d h d t d h ∣ ∣ ∣ ∣ h = 3 . 5 = 3 π r 2 h = 3 0 . 1 6 π h 3 = 0 . 1 6 π h 2 ⋅ d t d h = 0 . 1 6 π h 2 2 . 1 5 = 0 . 1 6 π ⋅ 3 . 5 2 2 . 1 5 ≈ 0 . 3 4 9 2 Note that h r = 1 0 4 ⟹ r = 0 . 4 h Note that d t d V = 2 . 1 5
I don't know if my solution is right or I just luckily arrived at the correct answer. hahahahahaha
V = 3 1 π r 2 h
r = 1 0 4 h or 5 2 h
V = 3 1 π ( 5 2 h ) 2 h
V = 7 5 4 π h 3
d t d V = 2 . 1 5
V = 2 . 1 5 t
2 . 1 5 t = 7 5 4 π h 3
h = ( 4 π 1 6 1 . 2 5 t ) 3 1
d t d h = 3 3 ( ( 4 π 1 6 1 . 2 5 t ) 2 ) 4 π 1 6 1 . 2 5
t = 1 6 1 . 2 5 4 π h 3
d t d h = 3 3 ( ( 4 π 1 6 1 . 2 5 ( 1 6 1 . 2 5 4 π h 3 ) ) 2 ) 4 π 1 6 1 . 2 5
d t d h = 1 2 π h 2 1 6 1 . 2 5
1 2 π ( 3 . 5 2 ) 1 6 1 . 2 5 = 0 . 3 4 9 1 6 6 4 5 7 . . . ≈ 0 . 3 4 9 2