Fluids with a pinch of calculus!

Let at time $t= t_0$ the height of water from the bottom be $y$ .

Using Torricelli's Theorem, Velocity of Efflux = $v_{bottom} = \sqrt{2\times g\times y}$

Implies:

Rate of flow of liquid is:

$\dfrac{dV_{bottom}}{dt} = a \times v_{bottom} = a\times\sqrt{2\times g\times y}$

Moving to the top:

The rate of descent of height of liquid is $-\d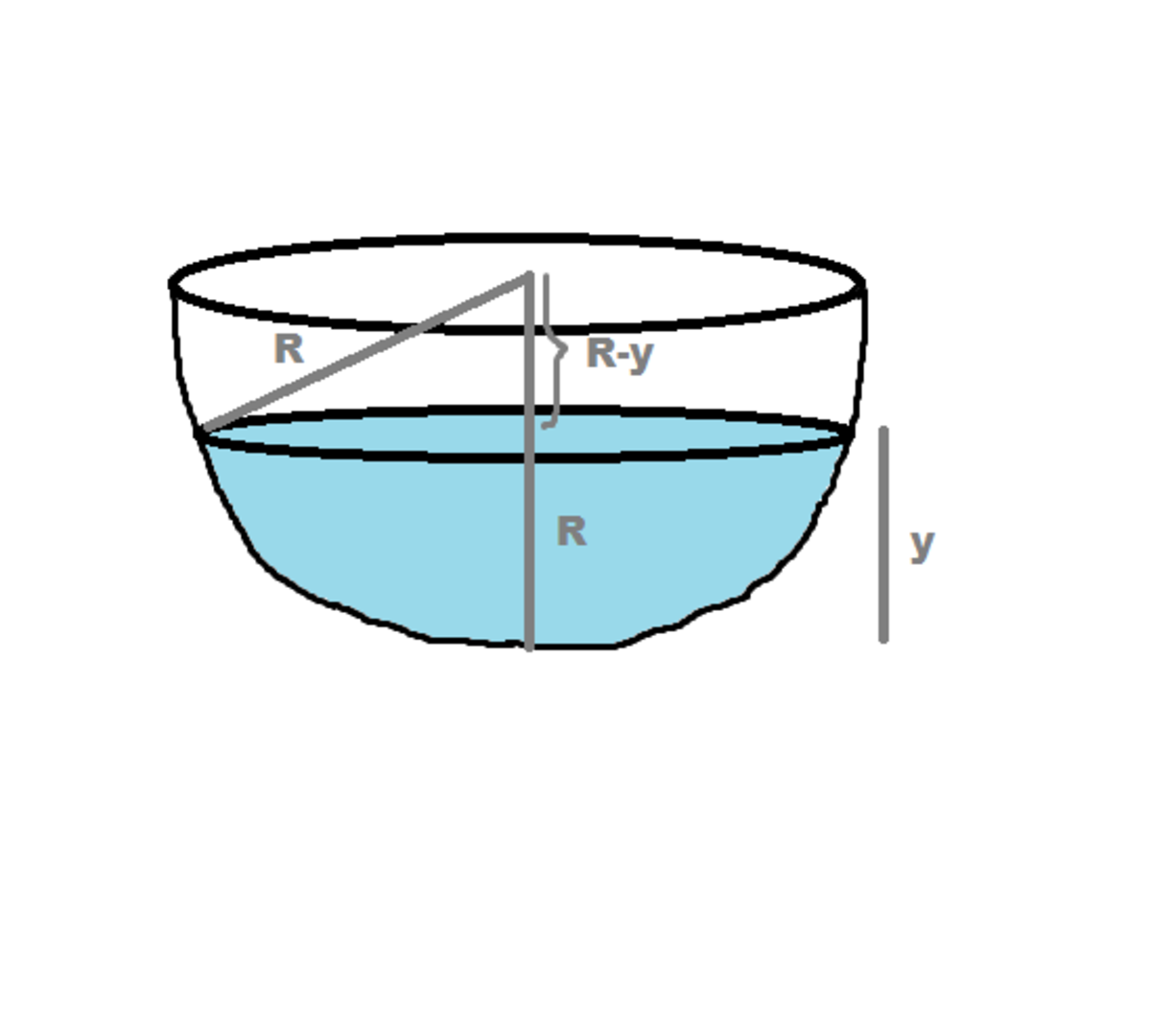frac{dy}{dt}$ From the diagram above:

Area of liquid is:

$A =\pi \times (R^{2} - (R-y)^{2})$

$A = \pi \times (2Ry - y^{2})$

Rate of loss of liquid is:

$\dfrac{dV_{top}}{dt} = -\dfrac{dy}{dt} \times A = -\dfrac{dy}{dt} \times \pi \times(2Ry - y^{2})$

Hence by equation of continuity: $\dfrac{dV_{top}}{dt} = \dfrac{dV_{bottom}}{dt}$

$-\dfrac{dy}{dt} \times \pi \times (2Ry - y^{2}) = a\times\sqrt{2\times g\times y}$

$-\dfrac{dy \times (2Ry - y^{2})}{\sqrt{y}} = \frac{a \times \sqrt{2\times g}}{\pi} dt$

$\int_{R}^{0} -(2R\sqrt{y} - y^{\frac{3}{2}}) \ dy= \int_{0}^{T} \frac{a\times \sqrt{2 \times g}}{\pi} \ dt$

On total simplification we get,

$T = \dfrac{14\pi \times R^{\frac{5}{2}}}{15 a \sqrt{2g}}$

After substitution: We get:

$T = \boxed{5994.50857}$

$\lfloor T \rfloor = \boxed{5994}$

Sum of digits = $5 + 9 + 9 + 4 = \boxed{27}$