Fluids+Efflux+Range
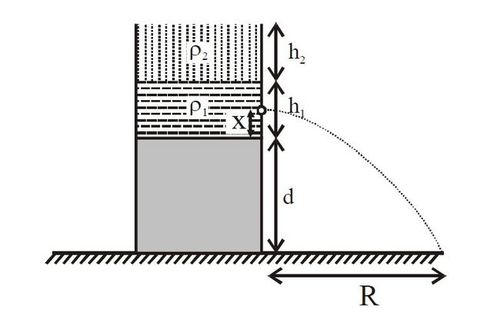 A vessel having two immiscible fluids having density
ρ
1
and
ρ
2
filled upto height
h
1
and
h
2
placed on a block of height
d
as shown in figure. There is a hole at a distance
x
from the bottom of vessel. For all
x
∈
(
0
,
h
1
)
if
x
increases, range
R
increases. Choose the correct relation.
A vessel having two immiscible fluids having density
ρ
1
and
ρ
2
filled upto height
h
1
and
h
2
placed on a block of height
d
as shown in figure. There is a hole at a distance
x
from the bottom of vessel. For all
x
∈
(
0
,
h
1
)
if
x
increases, range
R
increases. Choose the correct relation.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 A good problem.
Solution is given below.
A good problem.
Solution is given below.

This is some next level shit ! Beats !!!
I f t h e ρ 2 > ρ 1 t h e p r e s s u r e i s l e s s e f f e c t e d . ∴ ρ 1 ρ 2 > 1 . W e a r e i n t h e r a n g e 0 t o h 1 a b o v e d ∴ i t i s + h 1 .
I used mere observation .......actually it was very interesting . .
cheers to the challenge master
Log in to reply
@Nishant Rai what solution u have
@Niranjan Khanderia I couldn't understand your solution. Can you please explain me?