Flux through a cube corner
A point charge of charge q = 9 6 ϵ 0 is placed at one corner of a cube as shown. What is the electric flux through the shaded face?
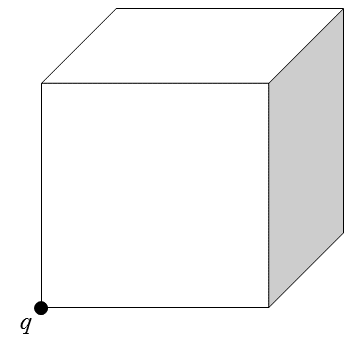
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
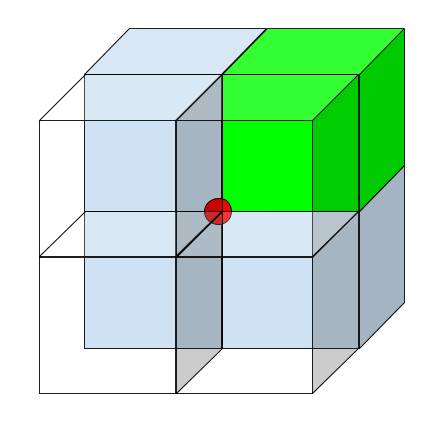 Imagine 8 cubes around a point charge. If you focus only 1 cube, the flux in that area would be
8
1
of total flux. Since the cube has only 3 sides that electric fields cross, then the flux of 1 side would be
2
4
1
of total flux. (The other 3 sides of the cube are parallel to the field, so there is no component that is perpendicular to those sides left.)
The answer would be
(
2
4
1
)
(
ϵ
0
q
)
=
(
2
4
1
)
(
ϵ
0
9
6
ϵ
0
)
=
4
.
Imagine 8 cubes around a point charge. If you focus only 1 cube, the flux in that area would be
8
1
of total flux. Since the cube has only 3 sides that electric fields cross, then the flux of 1 side would be
2
4
1
of total flux. (The other 3 sides of the cube are parallel to the field, so there is no component that is perpendicular to those sides left.)
The answer would be
(
2
4
1
)
(
ϵ
0
q
)
=
(
2
4
1
)
(
ϵ
0
9
6
ϵ
0
)
=
4
.
By Gauss' law , a surface containing the entire charge has total electric flux q / ϵ 0 = 9 6 . However, the cube as shown only contains one-eighth of the total flux. Furthermore, each of the three sides that contain non-zero flux has exactly one-third of the total flux of the cube. Therefore, the flux that goes through just one of the three sides is 9 6 / 2 4 = 4 .
You can consider a cube C centered at the origin and with length-side two. The flux is the equal to 96/6 over each of the six faces of such a cube. The area considered is one fourth of of the area of the face C and by simmetry we obtain flux=96/6/4=4