Flux Through Multi-Colored Disk

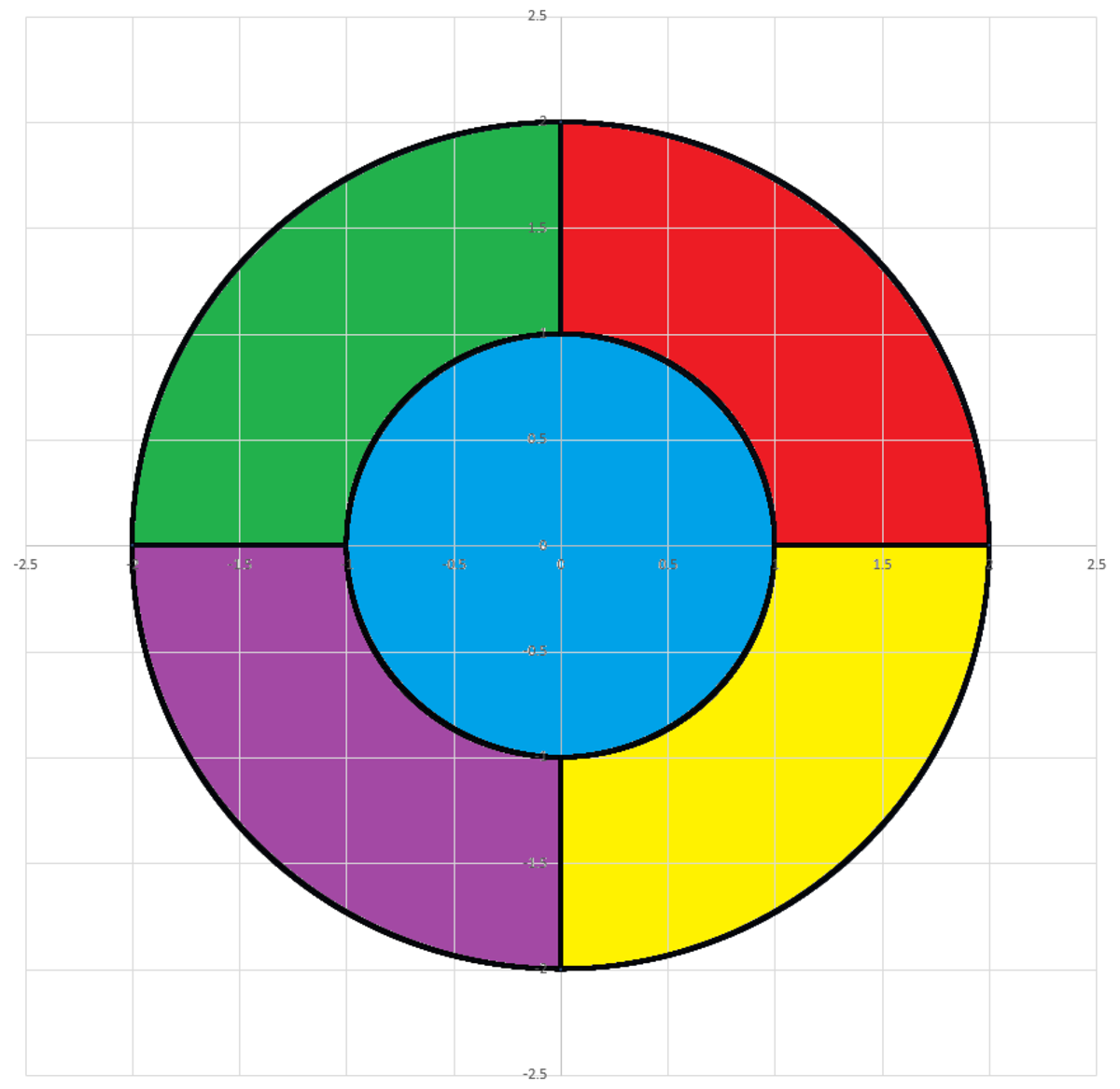
A particle with charge $q = +100$ is at position $(x,y,z) = (1,2,3)$ . There is a circular disk in the $xy$ plane, centered on the origin. The inner blue region has a radius of $1$ , and the disk as a whole has a radius of $2$ .

Let the electric fluxes through the five sub-surfaces be $\phi_B,\phi_R,\phi_G,\phi_P, \phi_Y$ .

Determine the following ratio:

$\frac{\phi_B \, \phi_R \, \phi_G \, \phi_P \, \phi_Y}{ \phi_B + \phi_R + \phi_G + \phi_P + \phi_Y}$

Inspiration

Details and Assumptions:
1) Electric permittivity $\epsilon_0 = 1$
2) All fluxes are positive