Focal triangle in an ellipse
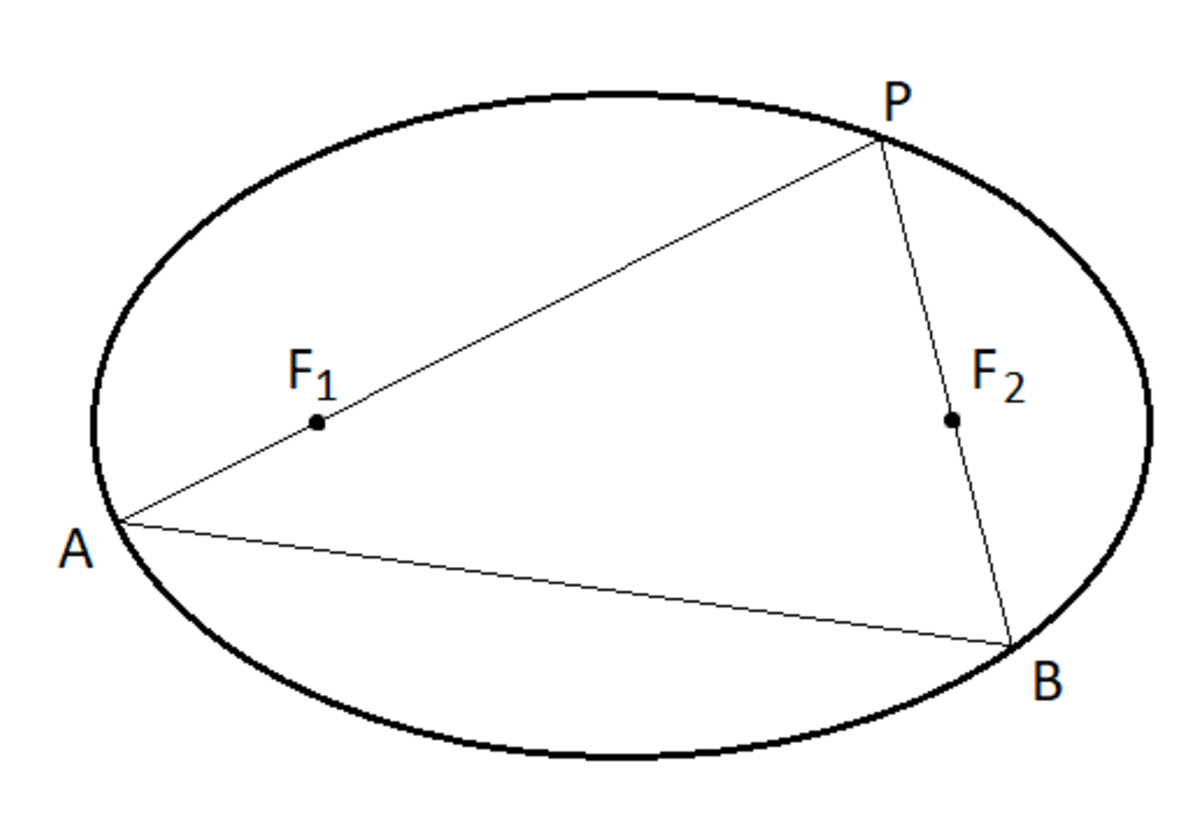
The ellipse shown in the figure above is given by 4 1 x 2 + y 2 = 1 . We select a point P randomly on the ellipse and connect the point P with the two foci F 1 and F 2 and extend the line segments to meet the ellipse again at A and B respectively. Find the maximum possible area of such a focal triangle.
The answer is 2.262.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
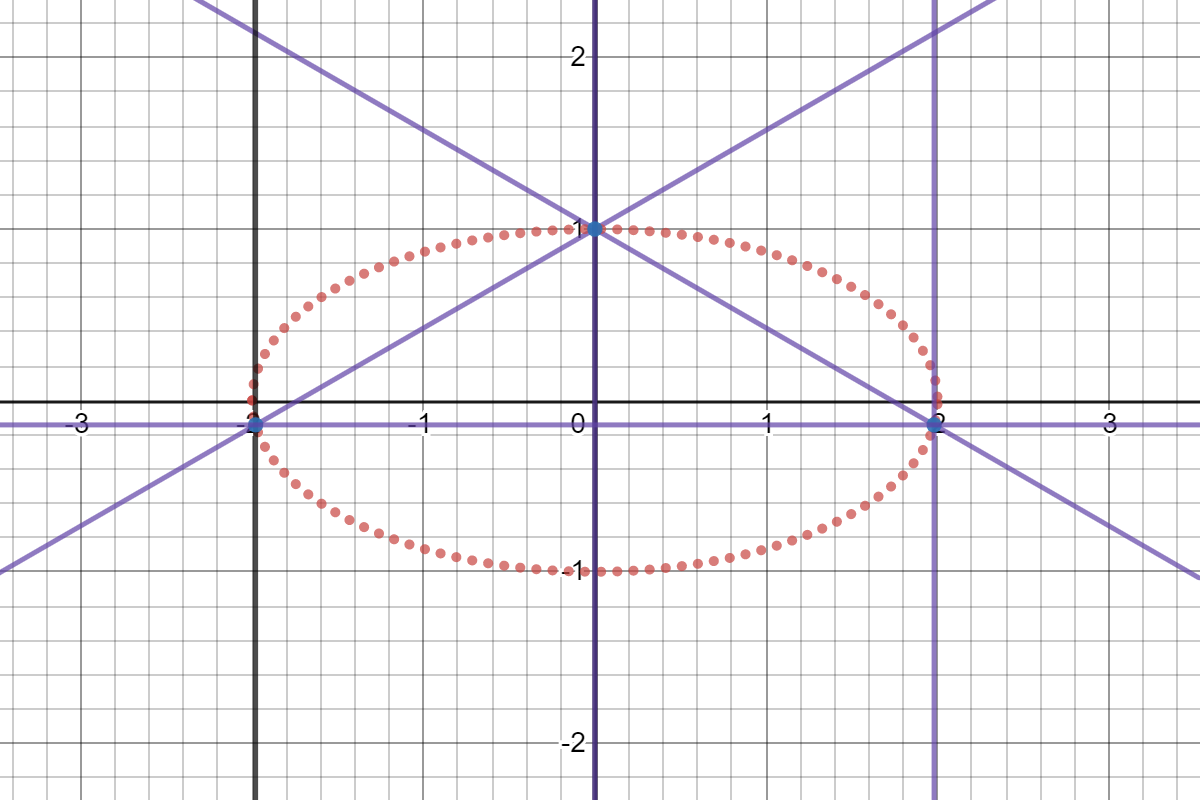
Solving equations and points given, we obtain three points that make up the triangle, ( 7 3 − 2 4 , 7 − 1 ) , ( 7 3 2 4 , 7 − 1 ) , ( 0 , 1 ) , and then find the sides of the triangle by distance formula, to use heron's formula for the area. See the graph and the equations obtained here
Note that F 1 , F 2 have coordinates ( − 3 , 0 ) and ( 3 , 0 ) respectively. If P has coordinates ( 2 cos t , sin t ) , the A , B have coordinates A : ( − 2 7 + 4 3 cos t 7 cos t + 4 3 , − 7 + 4 3 cos t sin t ) B : ( − 2 7 − 4 3 cos t 7 cos t − 4 3 , − 7 − 4 3 cos t sin t ) (solving simultaneously the equations of P F 1 and the ellipse, and of P F 2 and the ellipse), and hence P A B has area Δ ( t ) = 2 5 − 2 4 cos 2 t 8 3 sin t ( 5 − 3 cos 2 t ) using the fact that the triangle with vertices ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) has area equal to half the modulus of the determinant ∣ ∣ ∣ ∣ ∣ ∣ x 1 x 2 x 3 y 1 y 2 y 3 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ Elementary calculus shows that Δ ( t ) is maximised when t = 2 1 π , and Δ ( 2 1 π ) = 4 9 6 4 3 = 2 . 2 6 2 2 7 0 4 4 3