Focusing a beam of ions
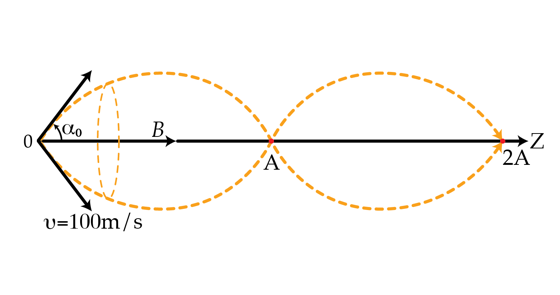
A source of ions at point O produces a slightly diverging beam with half-angle of divergence α 0 ≪ 1 . In order to collimate (re-focus) the beam, one can apply a uniform magnetic field along the z-axis (see the figure below). If all the ions have the same initial velocity and specific charge m q , the beam focuses at point A, again at point 2A and so on. Assuming that m q = 1 0 5 C/kg , B = 1 0 − 3 T , and v = 1 0 0 m/s , find the distance OA in meters .
The answer is 6.28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
First, consider the motion along the z -axis. The velocity of the particle along the z -axis is v cos α 0 , so the distance O A = t ⋅ v cos α 0 (let's call it ( ∗ ) ), where t is the time the particle needs to reach point A .
Next, consider the motion of the particle that is perpendicular to z -axis. In this case, the particle moves with velocity v sin α 0 . Since the particle is charged, it experiences the Lorentz force that is perpendicular to the velocity (the direction of the force is irrelevant in our case) given by F L = q v B sin α 0 .
This force makes the particle follow a circular path and imparts centripetal acceleration a = r v 2 . Using Newton's Second Law and the expression for the Lorentz force, we can derive the expression for the radius to be r = m q B v sin α 0 .
The time it takes for a particle to complete a loop is t = v sin α 0 2 π r . In our case, it is the same time that is required for a particle to reach point A along the z -axis. Therefore, we can substitute this expression for t into ( ∗ ) to find O A .
$$OA = \frac{v\cos{\alpha 0} 2\pi r}{v \sin{\alpha 0}} = \cot{\alpha 0} * 2\pi r = \cot{\alpha 0} * 2\pi \frac{v \sin{\alpha 0}}{\frac{q}{m} B} = 2 \pi \cos{\alpha 0} \frac{v}{\frac{q}{m} B}$$
Since α 0 ≪ 1 , we can use the small angle approximation and consider cos α 0 = 1 . Hence,
$$OA = \frac{2 \pi v}{\frac{q}{m} B} = \frac{2 * 3.14 * 100}{10^5 \cdot 10^{-3}} = 6.28 (m)$$
A = pitch = v c o s α 0 T = v q B 2 π m = 6 . 2 8 , as α 0 < < 1
We can divide this velocity vector into two components, v cos(alpha) and v sin(alpha). Since F = q (v x B) , the horizontal component i.e. v cos(alpha) will be unaffected by B, Only v sin(alpha) will be affected . The magnetic field will keep on changing the direction of v sin(alpha) and this component's locus will be circle, where q v sin(alpha) B = m v^2 sin^2 (alpha) /r
or r /v sin(alpha) = m/qB or 2pi r/v sin(alpha) = 2pi m/qB note that 2pi r/ v sin(alpha) is the time taken by particle to complete one revolution i.e. reach point A. Hence distance OA = v cos(alpha) * 2pi m/qB since alpha is very small, we can assume cos(alpha) = 1 , and now substituting the respective values of m/q,B and v, we get our desired answer i.e. 2pi
If any charged particle, say an electron is released in magnetic field with velocity at an angle α , it will undergo helical motion because of:
perpendicular component of velocity that makes electron undergo circular motion and parallel component of velocity along the magnetic field that remains unaffected.
Hence, r m v p e r p 2 = q v p e r p B
where, r = radius of circle q = charge of charged particle B = magnetic field strength m = mass of charged particle
therefore, v p e r p = m q b r
and T ,time period = v p e r p 2 π r = q B 2 π m
So, p i t c h = O A = distance moved in forward direction along the magnetic field
⇒ O A = v p a r a l l e l × T
= v cos α × q B 2 π m
v cos α = v because α ≪ 1 , assuming α ≈ 0
= v × 2 π q m × B 1
= 1 0 0 × 1 0 − 5 ⋅ 1 0 3 × 2 π
= 2 π
Therefore, O A = 2 π or 6.28 meters