Focusing on Incenters #3
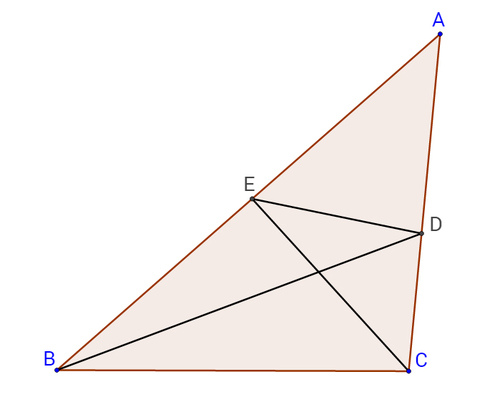 In
, the bisectors of
and
meet
and
at
and
respectively, and
. Find the value of
in degrees.
In
, the bisectors of
and
meet
and
at
and
respectively, and
. Find the value of
in degrees.
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
You have one degree of freedom here. So, you can arbitrarily set the value of ∠ A or ∠ B . Let, ∠ A = 4 0 ∘ . Then, you can easily get ∠ A D E = 1 0 0 ∘ ; ∠ A E D = 4 0 ∘ . Now, consider the triangle ADE only. Imagine a bisector of ∠ A . In this bisector O is a point such that ∠ D O E = 9 0 ∘ + 2 ∠ A = 1 1 0 ∘ . Hence, O is the incenter. Now, let ∠ O D E = α . You have to find the α for which ∠ D O E = 1 1 0 ∘ . This can be a daunting task. I used coordinate geometry to find α = 3 0 ∘ . Finally, 2 ∠ C = 3 0 ∘ + α ∠ C = 1 2 0 ∘ [P.S. Curious mind wants to know how the problem setter devised this ingenious problem!]