Folded Page Ⅱ
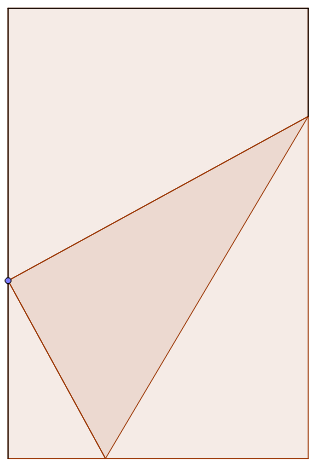
The lower corner of a leaf of unit width is folded over so as just to reach the opposite side of the page.
Find the width of the part folded over when the area folded over is minimum.
The answer is 0.666667.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the figure as shown. Then the width of the leaf C E = 1 . Let the width of the part folded over D E = B D = x and the angle between the crease A D and the right edge of the page A E , ∠ D A E = θ . There are many triangles similar to △ A D E . We note that B E = 2 x cos θ and that
cos θ ⟹ x = B E C E = 2 x cos θ 1 = 2 cos 2 θ 1
The folded-over area [ A B D ] = 2 1 A B ⋅ B D = 2 1 ⋅ tan θ x ⋅ x = 8 sin θ cos 3 θ 1 . [ A B D ] is minimum when f ( θ ) = sin θ cos 3 θ is maximum.
d θ d f ( θ ) ⟹ cos 2 θ tan θ ⟹ θ d θ 2 d 2 f ( θ ) = cos 4 θ − 2 sin 2 θ cos 2 θ = 3 sin 2 θ = 3 1 = 3 0 ∘ = − 4 sin θ cos 3 θ − 4 sin θ cos 3 θ + 4 sin 3 θ cos θ = − 4 5 3 < 0 Putting d θ d f ( θ ) = 0 Putting θ = 3 0 ∘
Therefore, f ( θ ) is maximum and [ A B D ] is minimum when θ = 3 0 ∘ or x = 2 cos 2 θ 1 = 3 2 = 0 . 6 6 7 .