Folding a charged triangle.
A thin uniformly charged dielectric plate has the shape of a right isosceles triangle. The plate is folded to obtain a similar triangle. The work required to fold the plate is W 1 = 1 J . What is the work in Joules W 2 required to fold it once more as in shown in the figure?
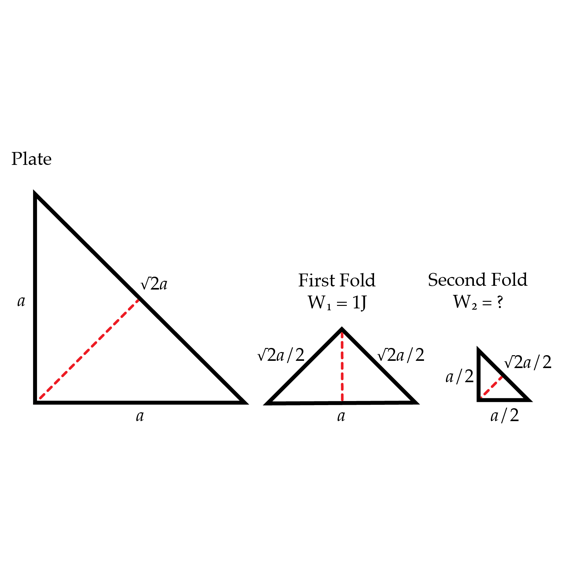
The answer is 1.41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
We can compute the work required to fold a right isosceles triangle by integration. For a triangle of height h and charge Q the answer should be of the form
W
=
C
h
Q
2
where C is an unknown constant. The problem becomes trivial when one realizes that C has the same value for all right isosceles triangles folded as in this problem. Note that the total charge of the triangle does not change when you fold it, i.e.
Q
1
=
Q
2
and therefore we can write
W
1
W
2
=
h
2
h
1
.
Basic trigonometry yields
h
2
h
1
=
2
and we arrive at the result
W
2
=
2
W
1
.
I assume that we have here a process which requires energy dissipated in the folding line of the dielectric material. And has nothing to do with it's dielectric properties:)
The 1Watt folding energy was dissipated on a folding line of a length(red broken line) computed as follows: Sqrt(a^2-b^2) where b=(sqrt(2)xa)/2= half length of the Hypotenuse of the leftmost triangle. The folding length thus is = a/sqrt(2) Using the Pythagorian theorem on the folded triangle(middle triangle) where the folding side is along the height(broken red line) . The Hypotenuse is (Sqrt(2)xa)/2 the base is a/2 which gives a height of a/2, this is the length of the folding line on which bending energy is spent. But this time we have to fold a two layered triangle, because of the previous folding, so the effective bending length will be 2xa/2=a, which if divided by a/Sqrt(2) length for 1watt spending will give us Sqrt(2)~ 1.4142watts about
work done in shearing along a length of say l is proportional to area lt where t is thickness of plate.In second fold,shear length is square root 2 times the first case.
Dice the original triangle into many tiny pieces that are essentially point charges with charge q . The electric potential energy of the original triangle would be the sum of the electric potential energy of all pairs of little pieces: 2 1 j = 1 ∑ i = 1 ∑ k q 2 / r i j where k is Coulomb's constant and r i j the distance between pieces i and j . Let's call the value of this sum X
The first folding is equivalent to reducing the distance between each pair of charges by a factor of 2 , so the energy after the first fold is 2 X .
2 X − X = 1 J
X = 3 . 4 1 4 2 . . . J
The second folding brings every pair closer again by a factor of 1 / 2 so energy difference before and after the second folding is given by:
2 X − 2 X = W 2
2 ( 3 . 4 1 4 2 ) − ( 2 ) 3 . 4 1 4 2 = W 2
2 J = W 2