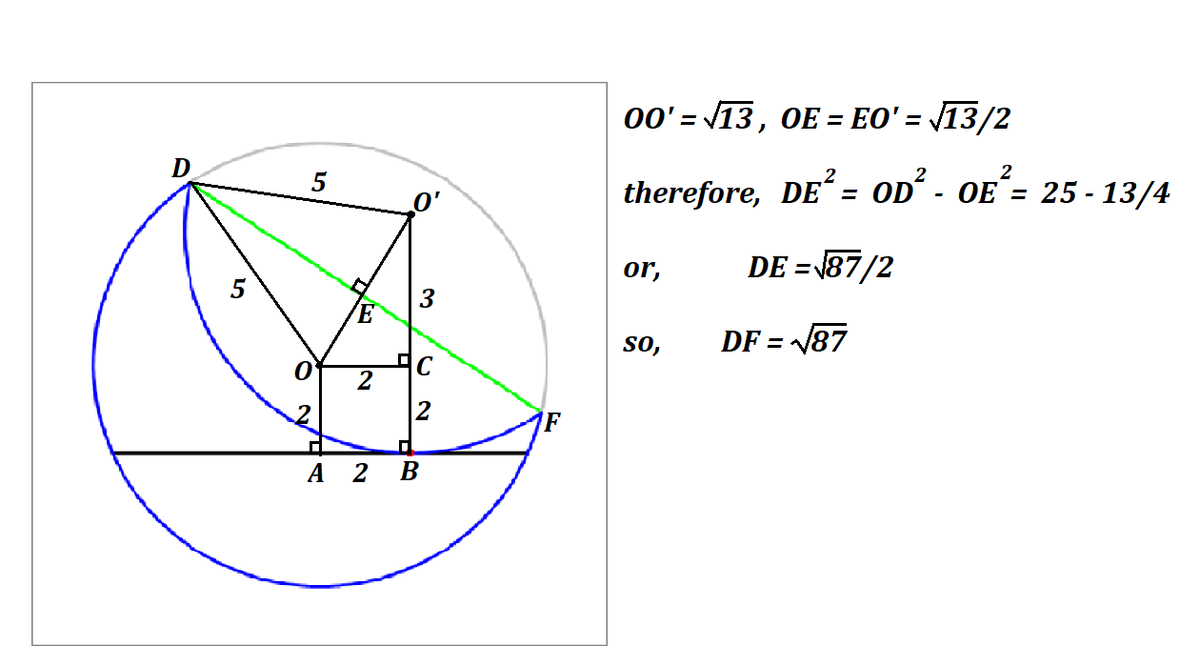
Folding a circle to touch a chord in it

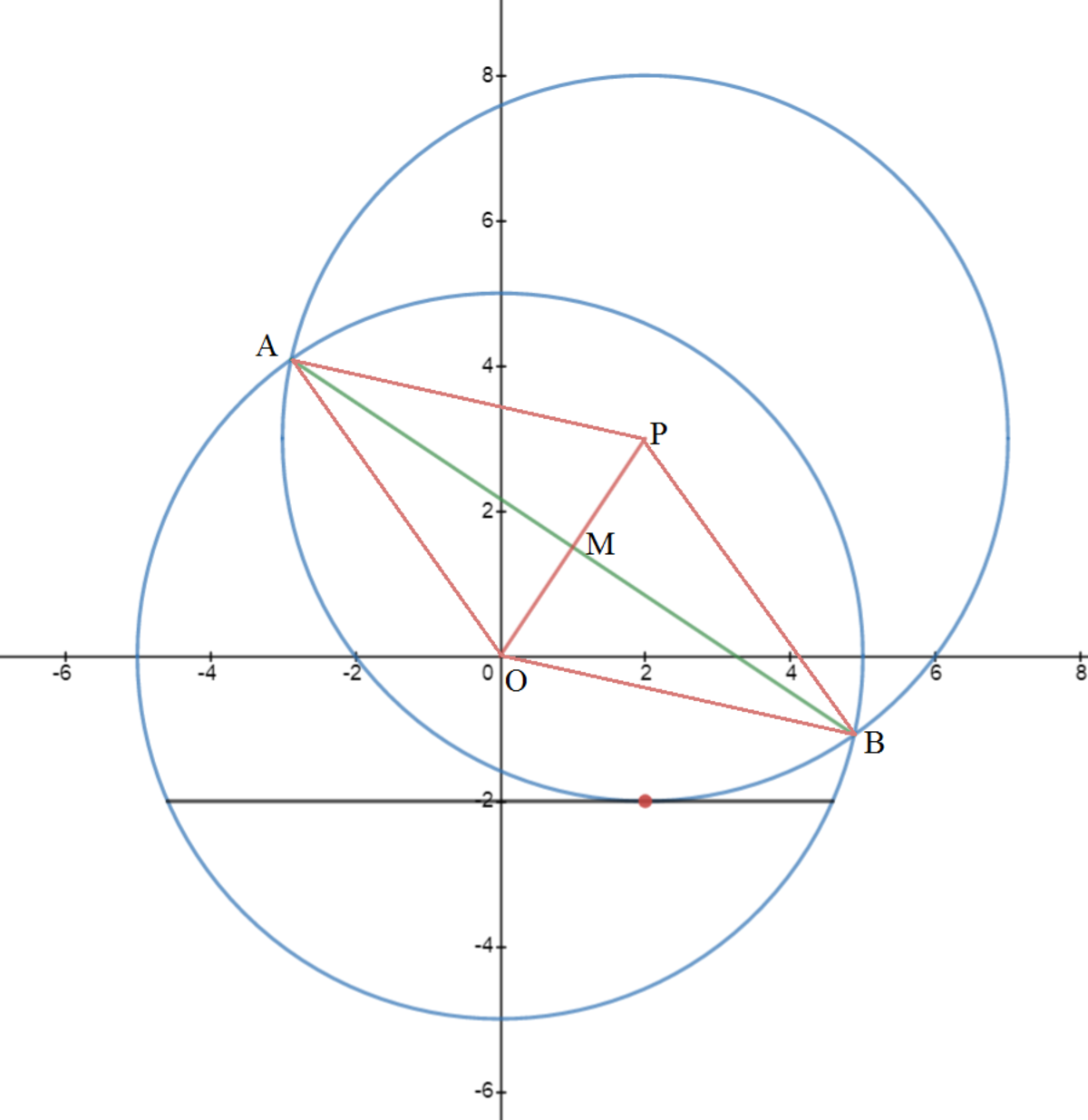
The original circle has its center at $O(0,0)$ and radius $5$ . The folded arc touches $y=-2$ at $(2,-2)$ . If we extend the folded arc to form a circle, the fold circle will have a radius of $5$ . Since the lowest point of the fold circle is $(2,-2)$ , its center is $P(2,3)$ . Let the end points of the fold be $A$ and $B$ . Then $\triangle AOP$ and $\triangle BOP$ are congruent isosceles with equal sides of length $5$ . Let $M$ be the midpoint of $OP$ , then

$\begin{aligned} AB &=2AM & \small \blue{\text{By Pythagorean theorem}} \\ & = 2\sqrt{AO^2-OM^2} \\ & = 2\sqrt{AO^2-\left(\frac {OP}2\right)^2} \\ & = 2\sqrt{5^2-\frac {(2-0)^2+(3-0)^2}{2^2}} \\ & = \sqrt{87} \end{aligned}$

Therefore $a=\boxed{87}$ .

Let the equation of the circle whose arc touches the line $y=-2$ be

$x^2+y^2+2gx+2fy+c=0$ .

Then, since the point $(2,-2)$ is on this circle, $8+4g-4f+c=0$ . Since the line $y=-2$ having zero slope is tangent to it,

$g+2=0\implies g=-2\implies c=4f$ .

Since radius of this circle is $5, g^2+f^2-c=5^2=25\implies f^2-4f-21=0\implies f=7,-3$ .

Since the center of the circle lies in the first quadrant, we choose $f=-3\implies c=-12$ .

So, the equation of the circle is $x^2+y^2-4x-6y-12=0$ , the equation of the common chord with the circle $x^2+y^2=25$ is $4x+6y=13$ , and the difference between the abscissa of it's end points is

$3\sqrt {\dfrac{87}{13}}$ ,

the difference between the ordinates is

$2\sqrt {\dfrac{87}{13}}$ .

Hence the length of the chord is

$\sqrt {\dfrac {9\times 87}{13}+\dfrac{4\times 87}{13}}=\sqrt {87}$ .

Hence $a=\boxed {87}$

Draw another circle with tangent at (2,-2). It will have a center at (2,3). Now you have two circles with centers at (0,0) and (2,3) with both radius equal to 5. The required length is the length of common chord which can be found by basic geometry.