Folding a square piece of paper

Geometry Level pending

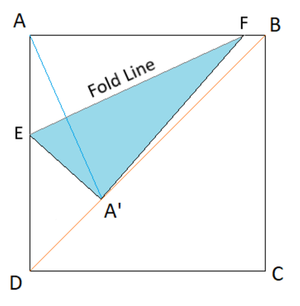
Given a square piece of paper of unit side length, you fold it such that one corner touches the opposite diagonal as illustrated by the above figure. If the folded segment is a triangle, what is its maximum possible area?


The answer is 0.2071.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Hosam Hajjir
Nov 21, 2020

Clearly, the maximum area is obtained when point F F is at corner B B , and in this case the fold line is the angle bisector of ∠ A B D \angle ABD .

Hence, A E ‾ = ( 1 ) tan ⁡ 22. 5 ∘ \overline{AE} = (1) \tan 22.5^{\circ} , and the maximum area = 1 2 tan ⁡ 22. 5 ∘ ≈ 0.2071 = \frac{1}{2} \tan 22.5^{\circ} \approx \boxed{0.2071}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...