Folding an ellipse
As shown in the figure, we have an ellipse of semi-major axis length along the horizontal direction, and semi-minor axis length along the vertical direction, centered at the origin. Next, we draw the line (the black chord). Now fold the upper part of the ellipse such that the folded part becomes tangent to the the black chord at (the red dot). Find the length of fold line (the green line segment). This problem requires the use of a numerical method. The image below does not represent the actual values specified above.
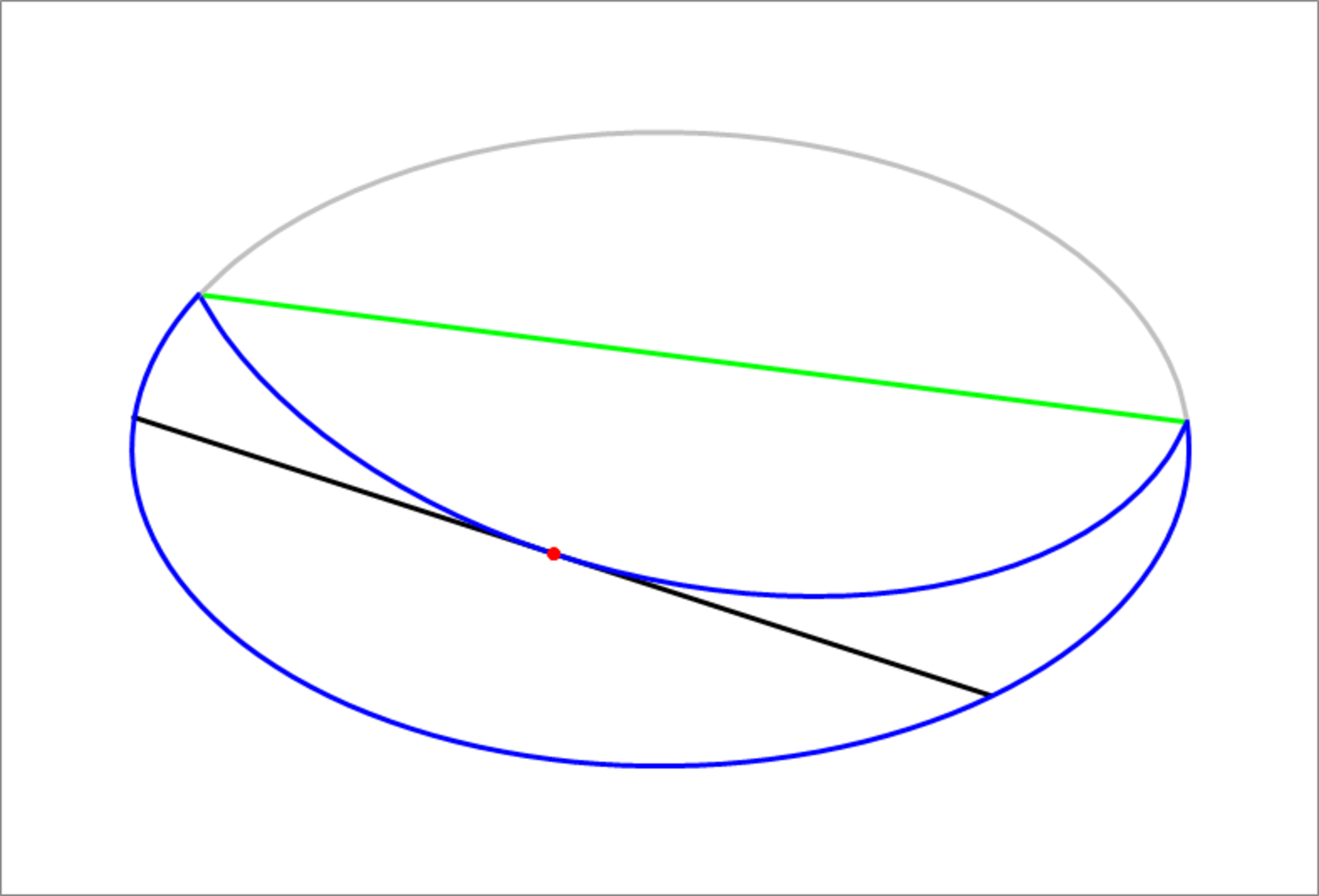
The answer is 8.394.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Extend the lines and label the points as below:
Since the black line is y = − 2 − x and P is at x = − 1 , the coordinates for P are P ( − 1 , − 1 ) .
Let the green line have an equation of y = m x + b . Then the green and black lines intersect at Q ( m + 1 − b − 2 , m + 1 b − 2 m ) .
P P ′ is perpendicular to the green line and through P ( − 1 , − 1 ) , so its equation is y = − m 1 ( x + 1 ) − 1 . It intersects the green line at R ( m 2 + 1 − 1 − m − m b , m 2 + 1 b − m − m 2 ) .
The coordinates for P ′ are then P ′ ( P x + 2 ( R x − P x ) , P y + 2 ( R y − P y ) ) or P ′ ( m 2 + 1 m 2 − 1 − 2 m − 2 m b , m 2 + 1 − m 2 + 1 + 2 b − 2 m ) .
The slope of Q P ′ is then m 2 = P x ′ − Q x P y ′ − Q y = − b m 2 − 2 b m + b + m 3 + m 2 − 3 m + 1 − b m 2 + 2 b m + b + m 3 − 3 m 2 + m + 1 .
The ellipse with semi-major axis 5 and semi-minor axis 3 has an equation of 2 5 x 2 + 9 y 2 = 1 . Using implicit differentiation, the slope of the tangent line on the ellipse is d x d y = − 2 5 y 9 x .
The reflected point P ′ must be on the ellipse, so 2 5 P x ′ 2 + 9 P y ′ 2 = 1 or
2 5 ( m 2 + 1 m 2 − 1 − 2 m − 2 m b ) 2 + 9 ( m 2 + 1 − m 2 + 1 + 2 b − 2 m ) 2 = 1
and the slope of Q P ′ must be the same as the slope of the tangent line of the ellipse at P ′ , so m 2 = − 2 5 P y ′ 9 P x ′ or
− b m 2 − 2 b m + b + m 3 + m 2 − 3 m + 1 − b m 2 + 2 b m + b + m 3 − 3 m 2 + m + 1 = − 2 5 ( m 2 + 1 − m 2 + 1 + 2 b − 2 m ) 9 ( m 2 + 1 m 2 − 1 − 2 m − 2 m b )
These two equations solve numerically to ( m , b ) ≈ ( − 0 . 4 7 9 3 9 3 , 0 . 9 5 0 4 9 ) for b > 0 , which means the green line has an approximate equation of y = − 0 . 4 7 9 3 9 3 x + 0 . 9 5 0 4 9 .
The green line and the ellipse then intersect at approximately ( − 3 . 0 1 2 1 7 , 2 . 3 9 4 5 ) and ( 4 . 5 5 7 2 5 , − 1 . 2 3 4 2 2 ) , which by the distance formula are approximately 8 . 3 9 4 units apart.