Folds and Creases-1

Geometry Level 5

A piece of paper is in the form of an equilateral triangle $ABC$ with side length $a$ . A fold is made such that vertex $A$ of the triangle meets a point $D$ on $AC$ such that $AD=\dfrac{a}{3}$ . Find the value of $k$ , if the perimeter of the resulting concave quadrilateral is $ka$ .

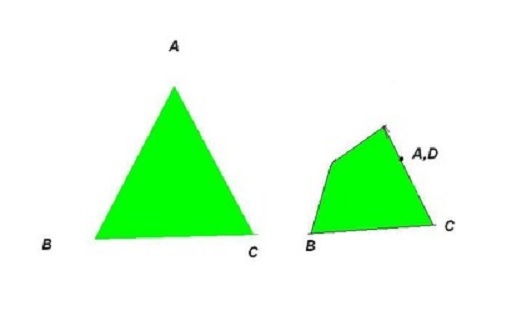
The answer is 2.78865.

1 solution

Ahmad Saad
May 4, 2017

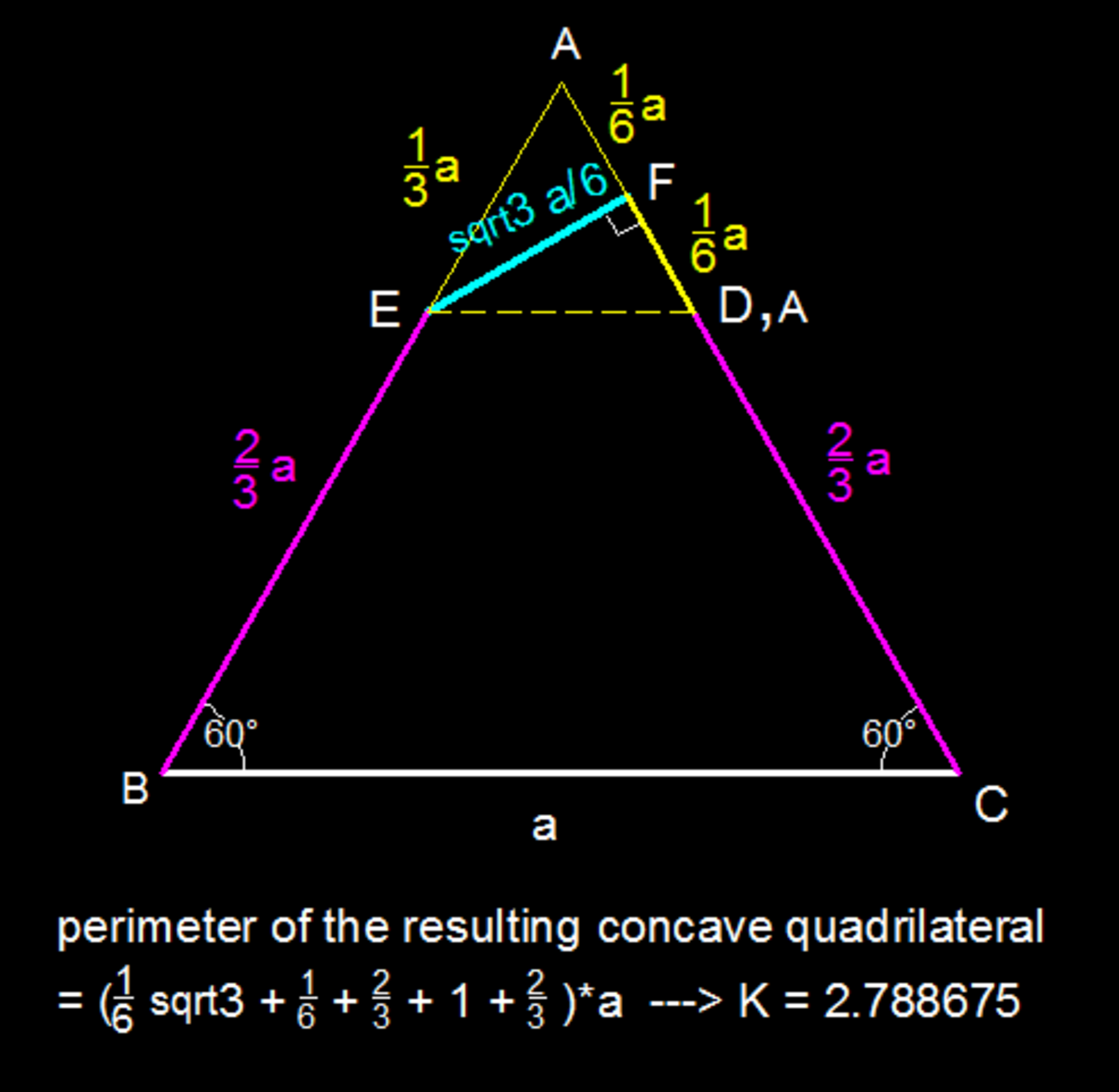
An eloquent diagram,indeed !

But why is FE perpendicular to AC?

Rohith M.Athreya - 4 years, 1 month ago

$A \hat{F} E = D \hat{F} E , \text{and} ~~ A \hat{F} E + ~ D \hat{F} E = 180^{ \circ}$

Sumanth R Hegde - 4 years, 1 month ago

As vertex "A" coincides point "D" along side AC ---> point "F" is a midpoint of AD such that AF = FD = AD/2 = a/6

sinse EF represents a folded line ---> Tr.AFE is congruent to Tr.DFE

<EDA = <EAD = 60 deg. , ED = EA ---> TR.EAD is an equilateral triangle

EF is a median ---> EF perpendicular to AD.

Ahmad Saad - 4 years, 1 month ago

Did almost the same way. $~ 3a-1/6-1/3+\sqrt3/2*1/3=2.78868.$ .AED is equilateral with side 1/3, and EF is the altitude.

Niranjan Khanderia - 4 years, 1 month ago