Follow the Charge
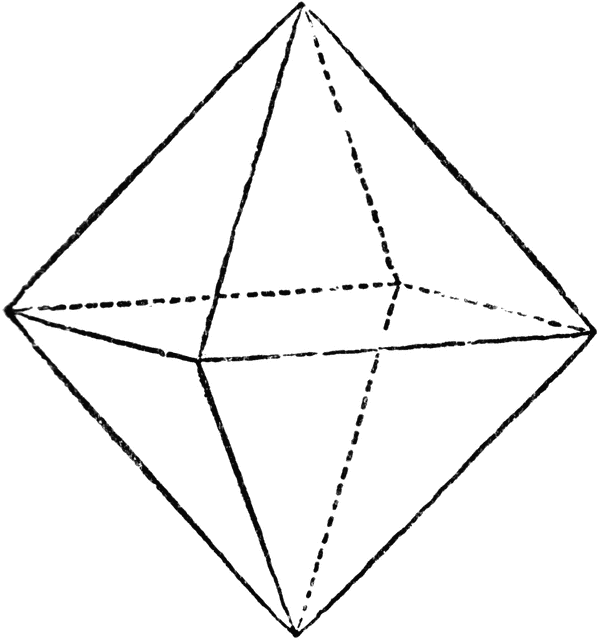 ⇒
S
i
x
p
o
i
n
t
−
l
i
k
e
u
n
i
t
c
h
a
r
g
e
s
a
r
e
f
i
x
e
d
a
t
t
h
e
v
e
r
t
i
c
e
s
o
f
a
r
e
g
u
l
a
r
O
c
t
a
h
e
d
r
o
n
i
n
s
u
c
h
a
w
a
y
t
h
a
t
o
p
p
o
s
i
t
e
v
e
r
t
i
c
e
s
c
o
n
t
a
i
n
o
p
p
o
s
i
t
e
c
h
a
r
g
e
s
.
⇒
T
h
e
O
c
t
a
h
e
d
r
o
n
i
s
t
h
e
n
f
i
x
e
d
a
t
a
c
e
r
t
a
i
n
p
o
s
i
t
i
o
n
i
n
s
p
a
c
e
.
⇒
A
l
l
t
h
e
e
d
g
e
s
o
f
t
h
e
O
c
t
a
h
e
d
r
o
n
a
r
e
e
a
c
h
o
f
l
e
n
g
t
h
2
Δ
.
⇒
I
p
l
a
c
e
a
u
n
i
t
t
e
s
t
c
h
a
r
g
e
a
t
a
n
a
r
b
i
t
r
a
r
y
p
o
i
n
t
i
n
s
p
a
c
e
s
u
c
h
t
h
a
t
i
t
s
E
l
e
c
t
r
i
c
P
o
t
e
n
t
i
a
l
E
n
e
r
g
y
i
s
V
0
.
⇒
I
t
h
e
n
s
u
b
s
e
q
u
e
n
t
l
y
d
r
a
g
t
h
e
t
e
s
t
c
h
a
r
g
e
,
V
E
R
Y
s
l
o
w
l
y
,
a
r
o
u
n
d
i
n
s
p
a
c
e
i
n
s
u
c
h
a
w
a
y
t
h
a
t
I
e
x
p
e
r
i
e
n
c
e
n
o
l
o
s
s
o
f
e
n
e
r
g
y
.
⇒
I
f
I
t
r
a
c
e
t
h
e
p
a
t
h
t
h
a
t
I
f
o
l
l
o
w
e
d
I
g
e
t
a
c
u
r
v
e
i
n
s
p
a
c
e
.
T
h
e
c
u
r
v
e
I
g
e
t
i
s
m
o
s
t
l
i
k
e
l
y
t
o
l
i
e
o
n
w
h
i
c
h
o
f
t
h
e
f
o
l
l
o
w
i
n
g
i
m
p
l
i
c
i
t
l
y
d
e
f
i
n
e
d
s
u
r
f
a
c
e
s
:
−
−
N
e
g
l
e
c
t
G
r
a
v
i
t
y
a
n
d
A
i
r
R
e
s
i
s
t
a
n
c
e
−
A
s
s
u
m
e
d
i
s
t
a
n
c
e
o
f
i
n
i
t
i
a
l
a
r
b
i
t
r
a
r
y
p
o
i
n
t
f
r
o
m
O
c
t
a
h
e
d
r
o
n
t
o
b
e
s
u
f
f
i
c
i
e
n
t
l
y
l
a
r
g
e
−
Δ
<
<
1
−
U
s
e
(
x
2
+
y
2
+
z
2
)
=
Γ
f
o
r
y
o
u
r
c
a
l
c
u
l
a
t
i
o
n
s
−
U
n
i
t
p
o
s
i
t
i
v
e
c
h
a
r
g
e
=
Q
−
P
e
r
m
i
t
t
i
v
i
t
y
o
f
f
r
e
e
s
p
a
c
e
=
Ω
(
A
)
z
=
Γ
[
2
(
Q
Δ
)
2
(
x
+
y
)
(
2
π
V
0
Ω
)
2
Γ
2
−
(
Q
Δ
)
2
]
−
(
x
+
y
)
x
y
(
B
)
z
2
=
[
(
3
Q
Δ
)
4
π
V
0
Ω
]
2
Γ
(
C
)
z
=
[
(
Q
Δ
)
2
π
V
0
Ω
]
2
Γ
3
−
(
x
+
y
)
(
D
)
z
=
Γ
(
4
π
2
Ω
2
V
0
2
)
[
9
(
Q
Δ
)
2
−
(
2
π
V
0
Ω
)
2
]
−
(
x
+
y
)
x
y
⇒
S
i
x
p
o
i
n
t
−
l
i
k
e
u
n
i
t
c
h
a
r
g
e
s
a
r
e
f
i
x
e
d
a
t
t
h
e
v
e
r
t
i
c
e
s
o
f
a
r
e
g
u
l
a
r
O
c
t
a
h
e
d
r
o
n
i
n
s
u
c
h
a
w
a
y
t
h
a
t
o
p
p
o
s
i
t
e
v
e
r
t
i
c
e
s
c
o
n
t
a
i
n
o
p
p
o
s
i
t
e
c
h
a
r
g
e
s
.
⇒
T
h
e
O
c
t
a
h
e
d
r
o
n
i
s
t
h
e
n
f
i
x
e
d
a
t
a
c
e
r
t
a
i
n
p
o
s
i
t
i
o
n
i
n
s
p
a
c
e
.
⇒
A
l
l
t
h
e
e
d
g
e
s
o
f
t
h
e
O
c
t
a
h
e
d
r
o
n
a
r
e
e
a
c
h
o
f
l
e
n
g
t
h
2
Δ
.
⇒
I
p
l
a
c
e
a
u
n
i
t
t
e
s
t
c
h
a
r
g
e
a
t
a
n
a
r
b
i
t
r
a
r
y
p
o
i
n
t
i
n
s
p
a
c
e
s
u
c
h
t
h
a
t
i
t
s
E
l
e
c
t
r
i
c
P
o
t
e
n
t
i
a
l
E
n
e
r
g
y
i
s
V
0
.
⇒
I
t
h
e
n
s
u
b
s
e
q
u
e
n
t
l
y
d
r
a
g
t
h
e
t
e
s
t
c
h
a
r
g
e
,
V
E
R
Y
s
l
o
w
l
y
,
a
r
o
u
n
d
i
n
s
p
a
c
e
i
n
s
u
c
h
a
w
a
y
t
h
a
t
I
e
x
p
e
r
i
e
n
c
e
n
o
l
o
s
s
o
f
e
n
e
r
g
y
.
⇒
I
f
I
t
r
a
c
e
t
h
e
p
a
t
h
t
h
a
t
I
f
o
l
l
o
w
e
d
I
g
e
t
a
c
u
r
v
e
i
n
s
p
a
c
e
.
T
h
e
c
u
r
v
e
I
g
e
t
i
s
m
o
s
t
l
i
k
e
l
y
t
o
l
i
e
o
n
w
h
i
c
h
o
f
t
h
e
f
o
l
l
o
w
i
n
g
i
m
p
l
i
c
i
t
l
y
d
e
f
i
n
e
d
s
u
r
f
a
c
e
s
:
−
−
N
e
g
l
e
c
t
G
r
a
v
i
t
y
a
n
d
A
i
r
R
e
s
i
s
t
a
n
c
e
−
A
s
s
u
m
e
d
i
s
t
a
n
c
e
o
f
i
n
i
t
i
a
l
a
r
b
i
t
r
a
r
y
p
o
i
n
t
f
r
o
m
O
c
t
a
h
e
d
r
o
n
t
o
b
e
s
u
f
f
i
c
i
e
n
t
l
y
l
a
r
g
e
−
Δ
<
<
1
−
U
s
e
(
x
2
+
y
2
+
z
2
)
=
Γ
f
o
r
y
o
u
r
c
a
l
c
u
l
a
t
i
o
n
s
−
U
n
i
t
p
o
s
i
t
i
v
e
c
h
a
r
g
e
=
Q
−
P
e
r
m
i
t
t
i
v
i
t
y
o
f
f
r
e
e
s
p
a
c
e
=
Ω
(
A
)
z
=
Γ
[
2
(
Q
Δ
)
2
(
x
+
y
)
(
2
π
V
0
Ω
)
2
Γ
2
−
(
Q
Δ
)
2
]
−
(
x
+
y
)
x
y
(
B
)
z
2
=
[
(
3
Q
Δ
)
4
π
V
0
Ω
]
2
Γ
(
C
)
z
=
[
(
Q
Δ
)
2
π
V
0
Ω
]
2
Γ
3
−
(
x
+
y
)
(
D
)
z
=
Γ
(
4
π
2
Ω
2
V
0
2
)
[
9
(
Q
Δ
)
2
−
(
2
π
V
0
Ω
)
2
]
−
(
x
+
y
)
x
y
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
T h e p r o b l e m e s s e n t i a l l y t a l k s a b o u t e q u i p o t e n t i a l s u r f a c e s . I f t h e c h a r g e w a s p l a c e d a t a n a r b i t r a r y p o i n t i n s p a c e a n d t h e n m o v e d a r o u n d i n s u c h a w a y t h a t r e q u i r e s n o e n e r g y t h e n t h a t p a t h m u s t l i e o n a n e q u i p o t e n t i a l s u r f a c e b e c a u s e t h e e l e c t r i c f i e l d i s p e r p e n d i c u l a r t o a l l p o i n t s o n s u c h a s u r f a c e a n d t h u s t h e w o r k t o b e d o n e a g a i n s t i t w o u l d b e z e r o . T h u s w e h a v e t o f i n d t h e e q u a t i o n o f t h e e q u i p o t e n t i a l s u r f a c e t h a t h a s p o t e n t i a l V 0 . T h e g e n e r a l f o r m u l a f o r p o t e n t i a l a t a n y p o i n t c a n b e c a l c u l a t e d c o n v e n t i o n a l l y b y c a l c u l a t i n g t h e i n d i v i d u a l p o t e n t i a l s d u e t o e a c h c h a r g e , s u m m i n g t h e m , a n d t h e n s o l v i n g t h e p r o b l e m a c c o r d i n g t o t h e c o n d i t i o n s g i v e n . H o w e v e r , t h i s i s v e r y t e d i o u s a n d c a n b e a v o i d e d i f w e m a k e a v e r y i n t e r e s t i n g o b s e r v a t i o n . T h e O c t a h e d r a l a r r a n g e m e n t o f c h a r g e s e s s e n t i a l l y c o n s i s t s o f t h r e e p a i r s o f o p p o s i t e c h a r g e s e a c h s e p a r a t e d b y a d i s t a n c e o f 2 Δ ( B y G e o m e t r y o f t h e O c t a h e d r o n ) a n d a l l p a i r s a r e p e r p e n d i c u l a r t o e a c h o t h e r a n d m e e t a t a c o m m o n p o i n t . I f w e a s s u m e t h i s c o m m o n p o i n t t o b e t h e o r i g i n o f a c o − o r d i n a t e s y s t e m , w e c a n t h e n a s s i g n t h e t h r e e a x e s a l o n g t h e t h r e e p a i r s o f c h a r g e s . F u r t h e r m o r e , s i n c e t h e d i s t a n c e Δ < < 1 a n d t h e i n i t i a l p o i n t i s a t a s u f f i c i e n t l y l a r g e d i s t a n c e f r o m t h e O c t a h e d r o n , t h e p a i r s o f c h a r g e s c a n b e a p p r o x i m a t e d t o b e h a v e a s d i p o l e s . T h u s , w e e n d u p w i t h t h r e e d i p o l e s , e a c h o r i e n t e d a l o n g a p a r t i c u l a r a x i s . N o w , w e a l r e a d y k n o w t h e p o t e n t i a l o f a d i p o l e o r i e n t e d a l o n g t h e z − a x i s , V = 4 π Ω R 2 Q ( d ) cos θ z w h e r e , cos θ z = R z a n d R 2 = ( x 2 + y 2 + z 2 ) = Γ S i m i l a r l y , c a l c u l a t i n g t h e p o t e n t i a l s d u e t o t h e o t h e r t w o d i p o l e s a n d t a k i n g d = 2 Δ , T h e t o t a l p o t e n t i a l Φ = 2 π Ω Γ 1 . 5 ( Q Δ ) ( x + y + z ) W e a l r e a d y k n o w t h a t w e w a n t t h e e q u a t i o n f o r t h e s u r f a c e t h a t i s e q u i p o t e n t i a l f o r p o t e n t i a l V 0 . T h u s , w e s e t Φ = V 0 T h i s w i l l g i v e u s t h e r e q u i r e d i m p l i c i t e q u a t i o n f o r t h e s u r f a c e w e w a n t ∵ Φ = V 0 ∴ 2 π Ω Γ 1 . 5 ( Q Δ ) ( x + y + z ) = V 0 W h i c h o n p r o p e r r e a r r a n g e m e n t g i v e s , z = Γ [ 2 ( Q Δ ) 2 ( x + y ) ( 2 π V 0 Ω ) 2 Γ 2 − ( Q Δ ) 2 ] − ( x + y ) x y