Follow The Fold
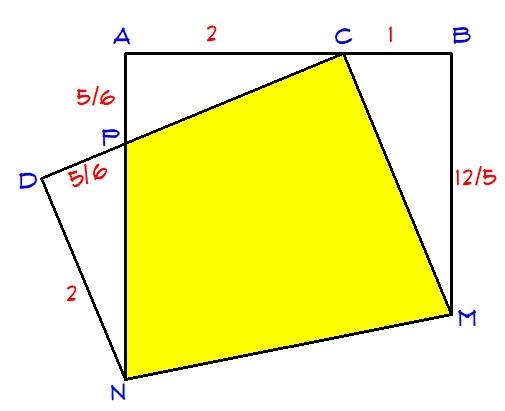
In rectangle ABCD (below left), A B = 3 and B C = 5 . The corner at C is folded up (below right) and lands on A B so that A C = 2 and C B = 1 .
The area of quadrilateral CPNM can be written as n m , where m and n are positive, coprime integers. Find m + n .
The answer is 106.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Nice solution indeed. I did it by calculating the area of all three side triangles and subtracting it from the total area of the paper before dividing that result by 2 to get the area of the quadrilateral.
nice solution.. i did it with coordinate geometry..
Log in to reply
can u please share ur solution using coordinate geometry...
very nice.....
Great solution. thank you!
great
is 15 a coprime integer ?as was mentioned in problem
Log in to reply
Being coprime isn't a quality of a single integer, but a quality of a pair of integers. Integers a and b being coprime means that g c d ( a , b ) = 1 .
 image
image
Δ M C B is a right triangle. So, C B 2 + B M 2 = M C 2 ⟹ 1 2 + x 2 = ( 5 − x ) 2 ⟹ x = 5 1 2
Δ M C B ∼ Δ C P A ⟹ B C A P = M B C A ⟹ A P = 6 5
Δ P A C is a right triangle. So, P A 2 + A C 2 = P C 2 ⟹ ( 6 5 ) 2 + 2 2 = P C 2 ⟹ P C = 6 1 3
C D = 3 ⟹ P D = 3 − 6 1 3 = 6 5
But, Δ P A C ∼ Δ P D N ⟹ Δ P A C ≃ Δ P D N ⟹ P N = P C = 6 1 3
Area of C P N M = A r . ( A B N M ) − A r . Δ A P C − A r . Δ B M C = 2 1 × 3 × ( 5 1 2 + 6 5 + 6 1 3 ) − 2 1 ( 2 × 6 5 ) − 2 1 ( 1 × 5 1 2 ) = 1 5 9 1
So, 9 1 + 1 5 = 1 0 6
very good ..... it is more understood to me with the help of a diagram
Very clear...
The idea is to compute B M and A P and hence areas of △ C B M and △ A C P and subtract it from area of rectangle A B C D which is 1 5 . We Write the C on A B as C 1 and that D after folding as D 1
Now, We notice that if B M = x then C 1 M = 5 − x . Hence, Pythagorus Theorem in △ B M C 1 , we have
B M 2 + C 1 B 2 = C 1 M 2
⟹ x 2 + 1 2 = ( 5 − x ) 2 . Solving we get B M = 5 1 2 and hence [ △ C 1 B M ] = 5 6
Moreover, if ∠ B C 1 M = θ , then, ∠ A C 1 P = ( 9 0 ∘ − θ ) . We have tan θ = 5 1 2 and hence A P A C 1 = cot ∠ A C 1 P = cot ( 9 0 ∘ − θ ) = tan θ = 5 1 2 . Solving, we get A P = 6 5 and [ △ A C 1 P ] = 6 5 .
Now, we need to find D N . For that, consider the right angled △ P N D 1 . Now, it is easy to observe that D 1 N ∥ C 1 M and A D ∥ B C and thus ∠ D 1 N P = ∠ B M C 1 . If we take D N = D 1 = y then we have P N = 5 − y − 6 5 . We have tan ∠ B M C 1 = 1 3 1 2 and hence P N D 1 N = 1 3 1 2 . Solving, we get D N = 2 .
Now we are left with computing the area of trapezium N D C M = 2 1 × sum of the parallel sides × distance between them .
We get,
[ N D C M ] = 2 1 × ( 2 + 5 1 3 ) × 3 = 1 0 6 9 . Hence,
[ C P N M ] = [ A B C D ] − [ A P C 1 ] − [ C 1 B M ] − [ N D C M ] = 1 5 − 6 5 − 5 6 − 1 0 6 9 = 1 5 9 1 . Hence the answer is 9 1 + 1 5 = 1 0 6
 Piece of ice cream!
Piece of ice cream!
A C P N M = 2 3 ( 5 ) − 2 1 ( 1 ) ( 5 1 2 ) − 2 ( 6 5 ) = 1 5 9 1
The desired answer is m + n = 9 1 + 1 5 = 1 0 6
Same as my solution . . .
Consider CN as a diameter, then A and D lies on this crcle. So, NDC and NAC are congruent triangle. So DPN and APC are congruent.
=> AP=5/6, CP=13/6
ACP and BMC are similar triangles and not congruent. Using BC=1(given).Find the area of BMC
All the areas are available now. Ans => 91/15 => 106
Almost same solution
To start, I will be calculating some length sizes in order to help me calculate the areas.
First of all, take a look at the triangle C B M . If B M is x , then C M is 5 − x ; and since CBM is a right triangle, we can use Pythagoras' Theorem to find x .
x 2 + 1 = ( 5 − x ) 2
x 2 + 1 = 2 5 − 1 0 x + x 2
1 0 x = 2 4
x = 2 . 4
Thus, B M = 2 . 4 and C M = 2 . 6
Now, take a look at the triangle A P C . If A B is a line and the angle P C M is a right angle, then the angle A C P is 9 0 ° − B C M and thus the angle A P C is equal to the angle B C M , and the triangles A C P and B C M are similar. Then, we can write: A P / A C = B C / B M . Then A P / 2 = 1 / 2 . 4 , so A P = 5 / 6
We can find PC by applying once more the Pythagorean Theorem:
A P 2 + A C 2 = P C 2
( 5 / 6 ) 2 + 2 2 = P C 2
2 5 / 3 6 + 4 = P C 2
P C = 1 3 / 6
Then D P = 3 − 1 3 / 6 = 5 / 6 .
Look now at triangle D P N . The angles D P N and A P C are opposite, and thus are equal; the angle P D N is right, so the angle P N D equals angle P C A , and so the triangles P D N and A P C are similar; furthermore, since P A = P D , the triangles are equal, thus D N = A C = 2 , and P N = 1 3 / 6 .
Seeing as the angles N D C and D C M are right, the quadrilateral D C M N is a trapezium, and its area is given by ( D N + C M ) ∗ D C / 2 = ( 2 + 2 . 6 ) ∗ 3 / 2 = 4 . 6 ∗ 3 / 2 = 6 . 9
The area of the triangle D P N is given by D P ∗ D N / 2 = 2 ∗ ( 5 / 6 ) / 2 = 5 / 6 .
The area of C P N M equals 6 . 9 − 5 / 6 = ( 6 9 / 1 0 − 5 / 6 ) = ( 2 0 7 / 3 0 − 2 5 / 3 0 ) = 1 8 2 / 3 0 = 9 1 / 1 5 . Thus, m = 9 1 , n = 1 5 , and the sum m + n equals 1 0 6 .
BM=x and CM=5-x using pythagorean theorem you can solve for x and it comes out to be 2.4. Triangles CBM and APC are similar by a ratio of 1.2 usinig this ratio you can calculate the sides of triangle APC. Then triangles APC and PDN are congruent. The length of side AN is 3 so extend line BM to make it length 3. Call the point to which you extend it R. Side RM is 3-2.4 which equals .6. Now take the sum of the areas of triangles RMN, CBM, and APC this gives you 88/30 subtract that from 270/30 and you get 91/15
Triangle CMB, Triangle PCA and triangle PND are similar. Starting with triangle CMB angle MCB = Theta We've got sideBC. The sum of sides BM + MC =5 Get Sin^{2}(theta) +Cos^{2}(theta)=1. Thus all sides of the triangle are known. For a level 4 it wont be difficult to proceed from here :D
O segredo é somar a área dos 3 triângulo, somá-las,depois subtrair da área do retângulo e dividir por 2. O motivo de dividir por dois é porque o papel foi dobrado.
- para achar a área dos triângulos temos que fazer semelhança entre eles, pois tem os mesmos ângulos.
I intend to calculate the area of C P N M by finding the area of trapezoid C D N M and subtracting the area of Δ P D N . So my formula is essentially
2 3 ( D N + C M ) − 2 1 ⋅ D P ⋅ D N .
If we let B M = x and C M = 5 − x , then the Pythagorean Theorem tells us that 1 + x 2 = ( 5 − x ) 2 . Solving this yields B M = x = 5 1 2 and C M = 5 1 3 .
It is straightforward to show that Δ C B M ∼ Δ P A C ∼ Δ P D N . This tells us that
P C = B M C M ⋅ A C = 1 2 1 3 ⋅ 2 = 6 1 3 ,
which means that D P = 3 − 6 1 3 = 6 5 . Using triangle similarity again, we see that
D N = C B B M ⋅ D P = 5 1 2 ⋅ 6 5 = 2 .
(Incidentally, this means that Δ P A C ≅ Δ P D N .) So now I can plug everything into my formula to get the area of C P N M :
2 3 ( 2 + 5 1 3 ) − 2 1 ⋅ 6 5 ⋅ 2 = 1 0 6 9 − 6 5 = 1 5 9 1 .
So the answer to the problem is 9 1 + 1 5 = 1 0 6 .