Foolish Electron in magnetic Field ...!!
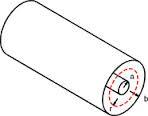Two co-axial conducting cylindrical shells having radius 'a' and 'b' (such that b>a).
A Uniform Magnetic field of strength 'B' is existing between cylindrical shells only which is directed along axis of cylinders.
An electron is emitted (ejected) by the inner shell in radially outward direction with velocity 'v'.
Find the MAXIMUM value of velocity 'v' so that this electron will not strike the outer cylindrical shell. ( Give answer in decimals upto 2 places )
Details and Assumptions:
1) Neglect all other forces except Magnetic forces.All values are in SI unit system.
2) ,e=charge on electron.
3) =mass of electron =
This is Part of set Foolish Things
Source :: Asked In My TesT
The answer is 3.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
V m a x = ( b 2 − a 2 ) e B / 2 b m . Hint: use Pythagoras theorem and maximum velocity occurs when electron just touches outer shell. (Since its solution is fully diagrammatic so I'am unable to post full solution )(also This Hint is sufficient enough since mathematical calculation is very less).