Proton inside a cyclotron
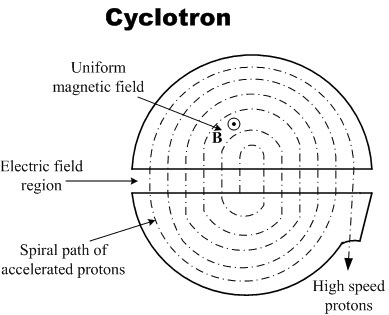 Consider a standard cyclotron accelerator in which two semi-circular regions (dees) are connected to an AC voltage source which provides an electric field
E
and a uniform vertical (out of the page) magnetic
B
field inside cyclotron which is perpendicular to the electric field. The electric field switches such that is always points toward the dee the particle is not in.
Consider a standard cyclotron accelerator in which two semi-circular regions (dees) are connected to an AC voltage source which provides an electric field
E
and a uniform vertical (out of the page) magnetic
B
field inside cyclotron which is perpendicular to the electric field. The electric field switches such that is always points toward the dee the particle is not in.
A proton is released from rest such that it starts rotating in the cyclotron at radius R and finally comes out from the slits of the cyclotron. The distance between the two semi-circular regions is d . Find the maximum number of turns proton take before coming out from slit's.
Details and Assumptions
m p = 1 . 6 × 1 0 − 2 7 kg q p = 1 . 6 × 1 0 − 1 9 C B = 1 0 − 4 T R = 6 m E = 1 0 m V d = 1 0 cm .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
nice solution man!
Very well done deepanshu
Great solution
Took twice of it counted 1 turn as one turn of the semicircle :P
this is the easiest way
It will exit the Dee when its radius is R (radius of Dee) or we need
m v / q B = R . now each time it crosses(equivalent of 1/2 turns) it gains an energy of q E d . , thus after n crosses it gets energy of n q E d = m v 2 / 2 .
Thus solve the two equations to get n as 1 8 . 0 2 2 . ..... now two crosses constitute one turn....hence 9 . 0 1 1 1 . whose box is 9 .
q e d is energy changed(potential)
Log in to reply
yeah so? energy changed = gain in kinetic energy?
I had edited the slight mistake of typing in your solution..!!
Log in to reply
oh was there a mistake,, i didnt notice,, thanks btw :)
i did only till 18 and was getting angry for not getting answer but ur solution helped me understand that mine was right
I missed the factor of 2 due to two crossings per turn, but otherwise did OK. But, I had to read "it starts rotating in the cyclotron at radius R" as "cyclotron OF radius R." Otherwise, you don't know the outer radius, and are left to assume the proton is injected at some intermediate radius R. Words are always a problem!
Number of turns will also depend on the point of release of proton.If it is released symmetrically then only this answer is correct.Nonethenless interesting question
I n e a c h t u r n t h a t p r o t o n m a k e , i t ′ s E n e r g y Δ E = 2 q p V W h e r e V = v o l t a g e a p p l i e d t o i t . s o T o t a l ↑ e s i n Δ E = n ( 2 q p V ) = n ( 2 q p E d ) a l s o Δ E = Δ K E ⟹ n ( 2 q p E d ) = 2 1 m p v m a x 2 ⟶ ( 1 ) s i n c e R = q p B m v m a x ⟶ ( 2 ) f r o m 1 & 2 n = 4 m p E d q p B 2 R 2 n = 9 A n s . .