for a good day of rest
Geometry
Level
4
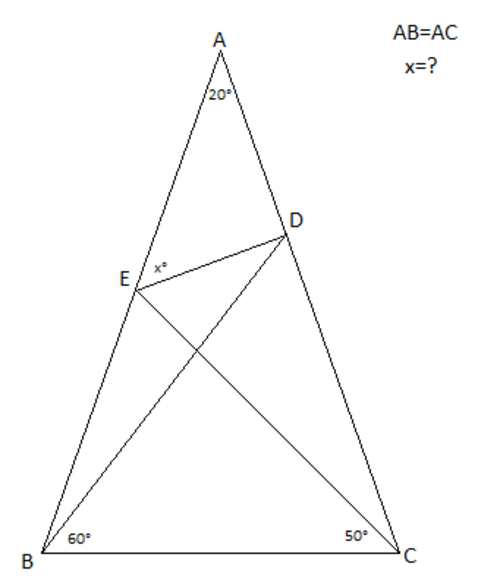 ABC is a triangle, AB=AC
DBC=60 degrees
ECB=50 degrees
BAC=20 degrees
ABC is a triangle, AB=AC
DBC=60 degrees
ECB=50 degrees
BAC=20 degrees
Find x° (AED angle).
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
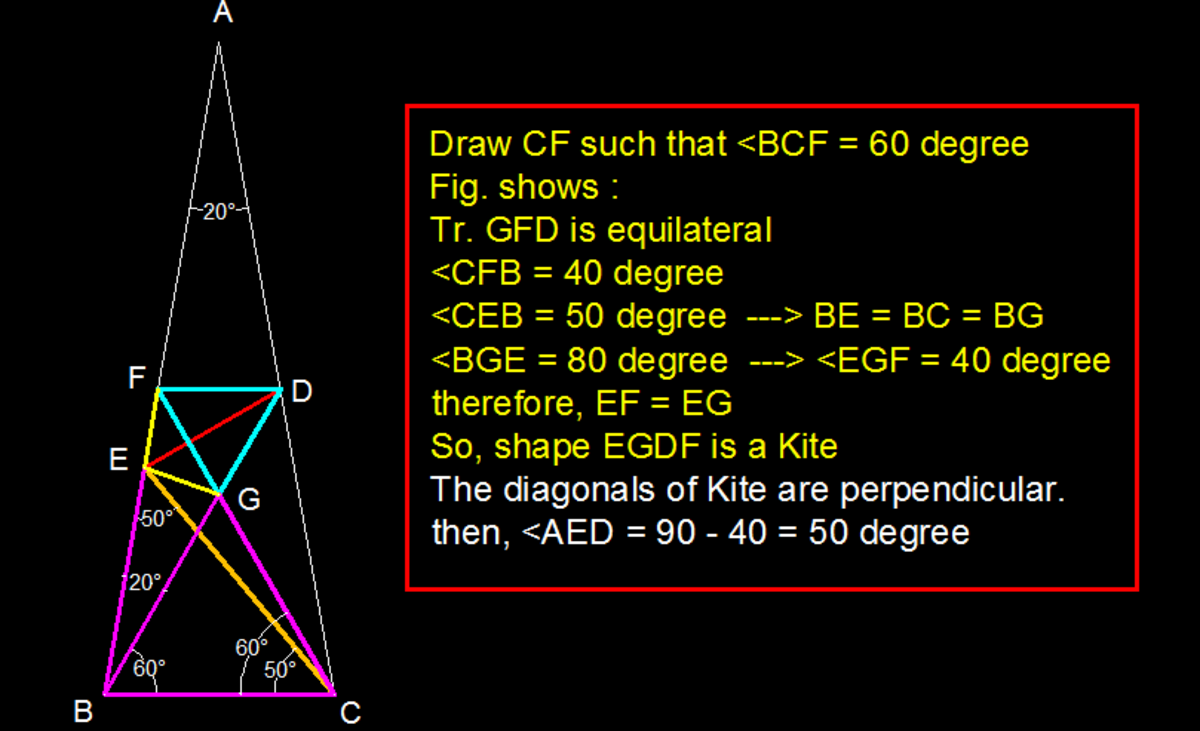
This is the famous problem Langley's Adventitious Angles where angle BDE=30. From there it is easy to get the answer.
Several solutions can be had from Google.com. Hence I am not putting them here. One such is given below.
link text