For lovers of 3D geometry - 2 (Area Calculations)
A right pyramid has a square base with side length 1 2 and a height of 1 0 . Along one of the edges of the base you pass a cutting plane bisecting the angle between the base and the triangular face joining that edge. The animation below illustrates this cut. Find the total area of the portion of the pyramid that lies below the cutting plane.
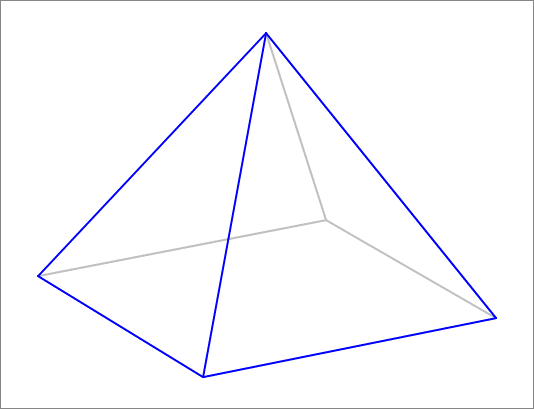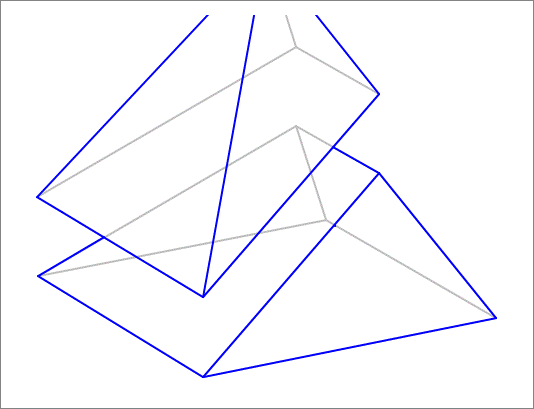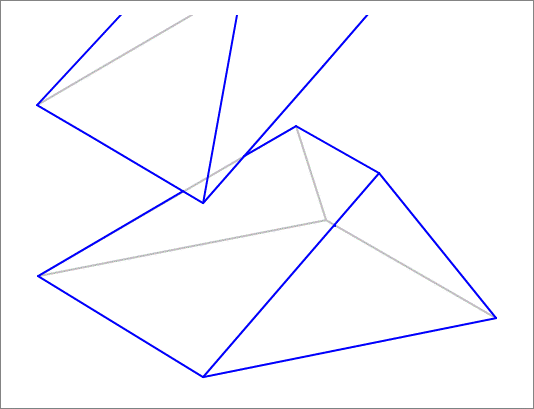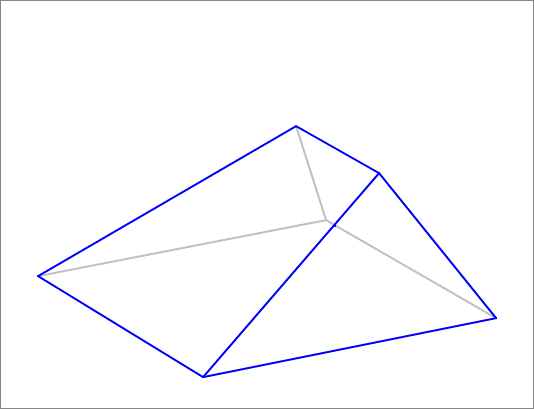
The answer is 360.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I just guessed the answer and got it right
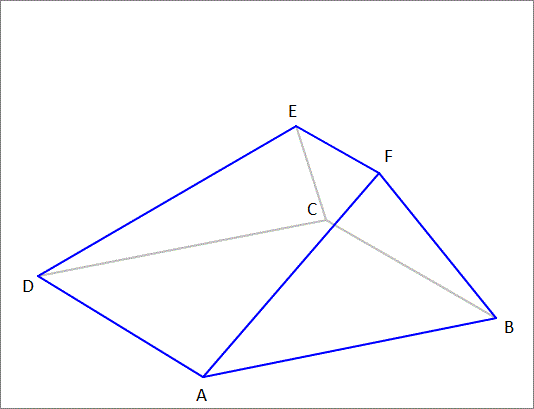
First, we'll label the vertices of the solid.
All we have to find are the coordinates of point F, and for that, we have to construct the equations of the three planes on which it lies. Assume point A is the origin of the x y plane, then point B = ( 1 2 , 0 , 0 ) . The angle between the triangular faces of the original pyramid and its base is θ 1 = tan − 1 6 1 0 = tan − 1 3 5 , while the angle between the cutting plane and the base is θ 2 = 2 1 θ 1
Therefore, the equations of the three planes meeting at point F are,
Plane F A B : ( 0 , − sin θ 1 , cos θ 1 ) ⋅ ( x , y , z ) = 0
Plane F B C : ( sin θ 1 , 0 , cos θ 1 ) ⋅ ( x − 1 2 , y , z ) = 0
Plane F A D : ( − sin θ 2 , 0 , cos θ 2 ) ⋅ ( x , y , z ) = 0
Solving the above system of 3 equations in the 3 unknowns results in,
F = ( x , y , z ) = ( 8 . 9 5 7 1 3 4 1 0 7 , 3 . 0 4 2 8 6 5 8 9 3 , 5 . 0 7 1 4 4 3 1 5 5 )
From symmetry, it follows that point E coordinates are given by
E = ( 8 . 9 5 7 1 3 4 1 0 7 , 1 2 − 3 . 0 4 2 8 6 5 8 9 3 , 5 . 0 7 1 4 4 3 1 5 5 ) = ( 8 . 9 5 7 1 3 4 1 0 7 , 8 . 9 5 7 1 3 4 1 0 7 , 5 . 0 7 1 4 4 3 1 5 5 )
We also have,
A = ( 0 , 0 , 0 ) , B = ( 1 2 , 0 , 0 ) , C = ( 1 2 , 1 2 , 0 ) , D = ( 0 , 1 2 , 0 )
The total area = [ A B C D ] + 2 [ F A B ] + [ A F E D ] + [ B C E F ]
[ A B C D ] = 1 2 2 = 1 4 4
[ F A B ] = 2 1 ∣ B × F ∣
[ A F E D ] = 2 1 ( ∣ F × E ∣ + ∣ E × D ∣ )
[ B C E F ] = 2 1 ( ∣ ( C − B ) × ( E − B ) ∣ + ∣ ( E − B ) × ( F − B ) ∣ )
Performing the above cross products and taking the magnitudes of the resulting vectors and adding it all up, we get
Total Area = 3 6 0 . 1 4 3 6 1 ≈ 3 6 0 . 1
Let △ A B C be the cross-section of the pyramid, and label the points and segments as follows:
By the Pythagorean Theorem on △ A M C , l = h 2 + ( 2 s ) 2 = 2 1 4 h 2 + s 2 .
By the angle bisector theorem, A B A C = B P C P , or s l = k l − k , which solves to k = s + l s l .
Since △ B N P ∼ △ B M C by AA similarity, B P N P = B C C M , or k h 2 = l h , which solves to h 2 = l h k . Also, B N N P = B M C M , or p h 2 = 2 s h , which solves to p = 2 h s h 2 .
By the Pythagorean Theorem on △ A N P , j = h 2 2 + ( s − p ) 2 .
Now we'll transfer the variables to the three-dimensional picture of the the lower pyramid:
The total surface area of the lower pyramid is the sum of the area of the square base, the area of the two congruent side triangles, and the areas of the large and small trapezoids, or A pyramid = A square + 2 A triangle + A large trapezoid + A small trapezoid = s 2 + 2 ⋅ 2 1 s p 2 + h 2 2 + 2 1 j ( s + s − 2 p ) + 2 1 k ( s + s − 2 p ) , or:
A pyramid = s 2 + s p 2 + h 2 2 + j ( s − p ) + k ( s − p ) .
In this question, s = 1 2 and h = 1 0 , so:
l = 2 1 4 h 2 + s 2 = 2 1 4 ⋅ 1 0 2 + 1 2 2 = 2 3 4
k = l + s l s = 1 2 + 2 3 4 1 2 ⋅ 2 3 4 = − 2 0 4 + 3 6 3 4
h 2 = l h k = 2 3 4 1 0 ( − 2 0 4 + 3 6 3 4 ) = 1 8 0 − 3 0 3 4
p = 2 ⋅ 1 0 1 2 ⋅ ( 1 8 0 − 3 0 3 4 ) = 1 0 8 − 1 8 3 4
j = h 2 2 + ( s − p ) 2 = ( 1 8 0 − 3 0 3 4 ) 2 + ( 1 2 − ( 1 0 8 − 1 8 3 4 ) ) 2 = 1 2 5 7 8 − 9 9 3 4
A pyramid
= s 2 + s p 2 + h 2 2 + j ( s − p ) + k ( s − p )
= 1 2 2 + 1 2 ( 1 0 8 − 1 8 3 4 ) 2 + ( 1 8 0 − 3 0 3 4 ) 2 + ( 1 2 5 7 8 − 9 9 3 4 ) ( 1 2 − ( 1 0 8 − 1 8 3 4 ) ) + ( − 2 0 4 + 3 6 3 4 ) ( 1 2 − ( 1 0 8 − 1 8 3 4 ) )
≈ 3 6 0 . 1 .