For lovers of 3D geometry
A right pyramid has a square base with side length 1 2 and a height of 1 0 . Along one of the edges of the base you pass a cutting plane bisecting the angle between the base and the triangular face joining that edge. The animation below illustrates this cut. Find the volume of the pyramid that lies below the cutting plane.
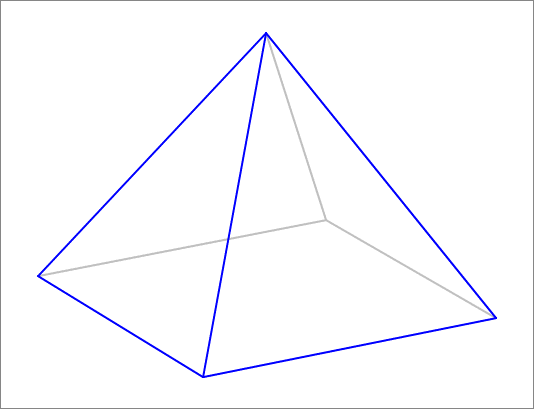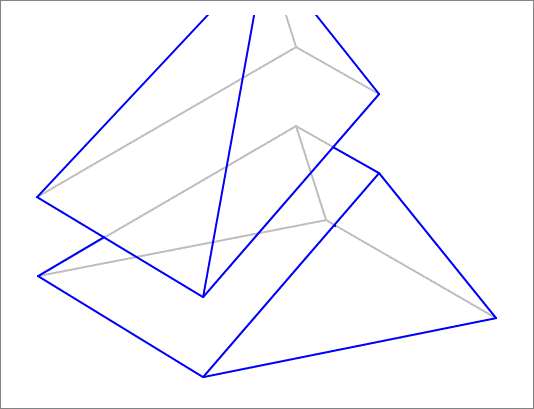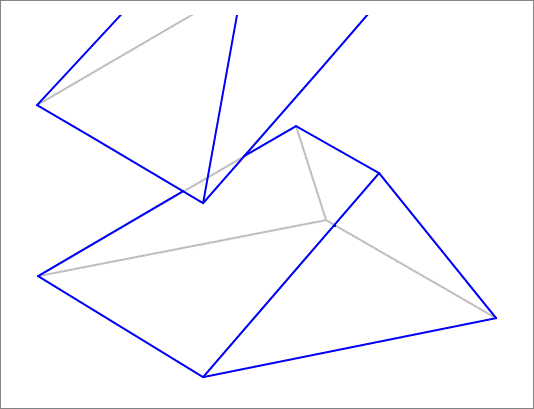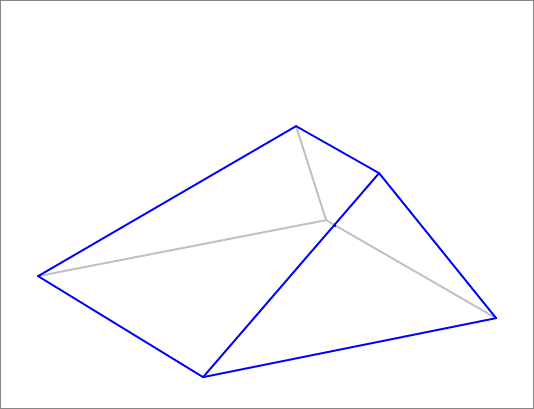
The answer is 303.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Fine. What software do you use for picture?
Log in to reply
MS-Excel (Chart) plus gifmaker.org to assemble the frames of the animation.
Let △ A B C be the cross-section of the pyramid, and label the points and segments as follows:
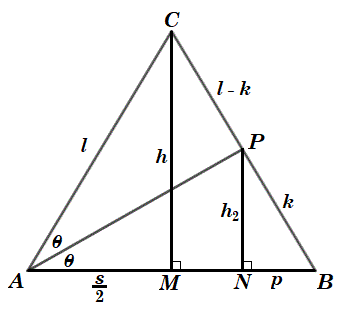
By the Pythagorean Theorem on △ A M C , l = h 2 + ( 2 s ) 2 = 2 1 4 h 2 + s 2 .
By the angle bisector theorem, A B A C = B P C P , or s l = k l − k , which solves to k = s + l s l .
Since △ B N P ∼ △ B M C by AA similarity, B P N P = B C C M , or k h 2 = l h , which solves to h 2 = l h k . Also, B N N P = B M C M , or p h 2 = 2 s h , which solves to p = 2 h s h 2 .
Now consider the lower pyramid encased in a right triangular prism:
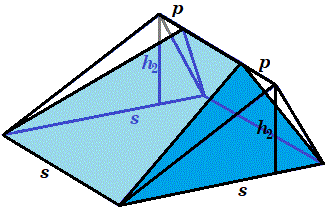
The volume of the lower pyramid is the volume of the right triangular prism minus twice the volume of the side tetrahedra with perpendicular sides s , h 2 , and p , or V pyramid = V prism − 2 V tetrahedron = 2 1 h 2 s 2 − 2 ⋅ 6 1 h 2 p s , or:
V pyramid = 6 1 h 2 s ( 3 s − 2 p ) .
In this question, s = 1 2 and h = 1 0 , so:
l = 2 1 4 h 2 + s 2 = 2 1 4 ⋅ 1 0 2 + 1 2 2 = 2 3 4
k = l + s l s = 1 2 + 2 3 4 1 2 ⋅ 2 3 4 = − 2 0 4 + 3 6 3 4
h 2 = l h k = 2 3 4 1 0 ( − 2 0 4 + 3 6 3 4 ) = 1 8 0 − 3 0 3 4
p = 2 ⋅ 1 0 1 2 ⋅ ( 1 8 0 − 3 0 3 4 ) = 1 0 8 − 1 8 3 4
V pyramid = 6 1 h 2 s ( 3 s − 2 p ) = 6 1 ( 1 8 0 − 3 0 3 4 ) 1 2 ( 3 ⋅ 1 2 − 2 ( 1 0 8 − 1 8 3 4 ) ) = − 1 3 8 2 4 0 + 2 3 7 6 0 3 4 ≈ 3 0 3 . 4 .
After substituting the above values for l , k , h 2 , and p , the general equation for the volume of the pyramid can also be simplified to:
V pyramid = 3 ( 4 h 2 − 3 s 2 ) 2 8 h s 4 ( s 2 − 4 h 2 ) + h s 3 ( 1 2 h 2 − s 2 ) 4 h 2 + s 2
in terms of side s and height h .
First, we'll label the vertices of the solid. The volume of the solid can be split into three parts, one triangular prism in the middle, and two rectangular pyramids on each side (which are mirror images of each other).
All we have to find are the coordinates of point F, and for that, we have to construct the equations of the three planes on which it lies. Assume point A is the origin of the x y plane, then point B = ( 1 2 , 0 , 0 ) . The angle between the triangular faces of the original pyramid and its base is θ 1 = tan − 1 6 1 0 = tan − 1 3 5 , while the angle between the cutting plane and the base is θ 2 = 2 1 θ 1
Therefore, the equations of the three planes meeting at point F are,
Plane F A B : ( 0 , − sin θ 1 , cos θ 1 ) ⋅ ( x , y , z ) = 0
Plane F B C : ( sin θ 1 , 0 , cos θ 1 ) ⋅ ( x − 1 2 , y , z ) = 0
Plane F A D : ( − sin θ 2 , 0 , cos θ 2 ) ⋅ ( x , y , z ) = 0
Solving the above system of 3 equations in the 3 unknowns results in,
F = ( x , y , z ) = ( 8 . 9 5 7 , 3 . 0 4 3 , 5 . 0 7 1 )
Therfore, the volume is given by
V = 2 1 ( 1 2 ) ( 5 . 0 7 1 ) ( 1 2 − 2 ( 3 . 0 4 3 ) ) + 3 2 ( 1 2 ) ( 3 . 0 4 3 ) ( 5 . 0 7 1 ) = 3 0 3 . 4