For Pi Han Goh and Chris Lewis, since you asked the question that led to this problem.

Algebra Level 5

Pi Han Goh and Chris Lewis asked the question of from where did I get the Approximate the answer based on distances between SSS triangles' upper vertices problem. Those data came from a web search on the phrase "almost integer". There was an implication that finding such triangles was difficult. It was not. It was computationally intensive though. That is strictly background.

Here is the graphic from the other problem. The markings are similar in this problem.

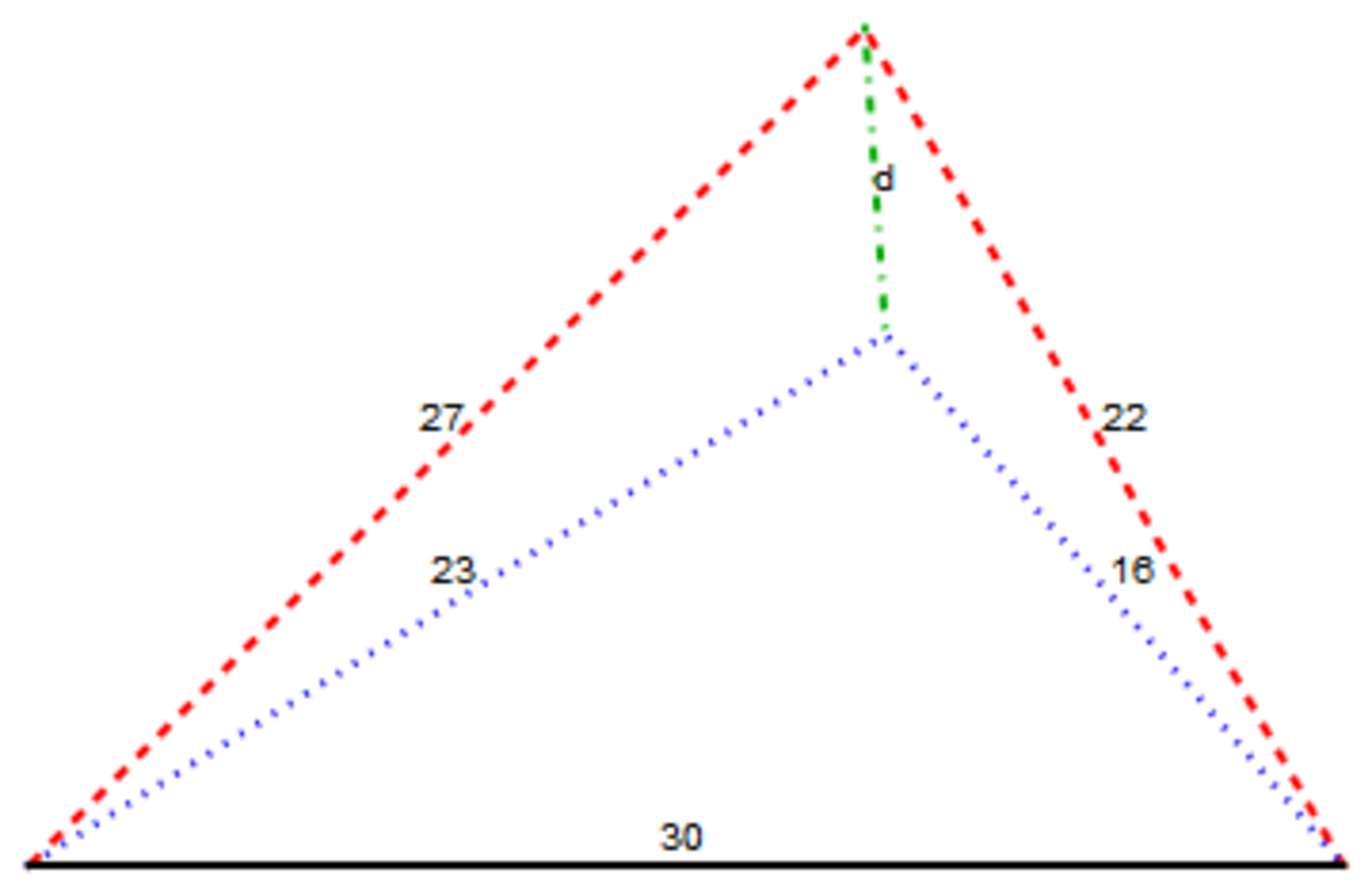
Now, this problem compares the $d_1$ and the $d_2$ distances as described below.

2020-10-11T14:41Z: Because, some people had commented that the diagram was difficult to understand, I am adding another version that I hope will help. It contains the same information spread out more.

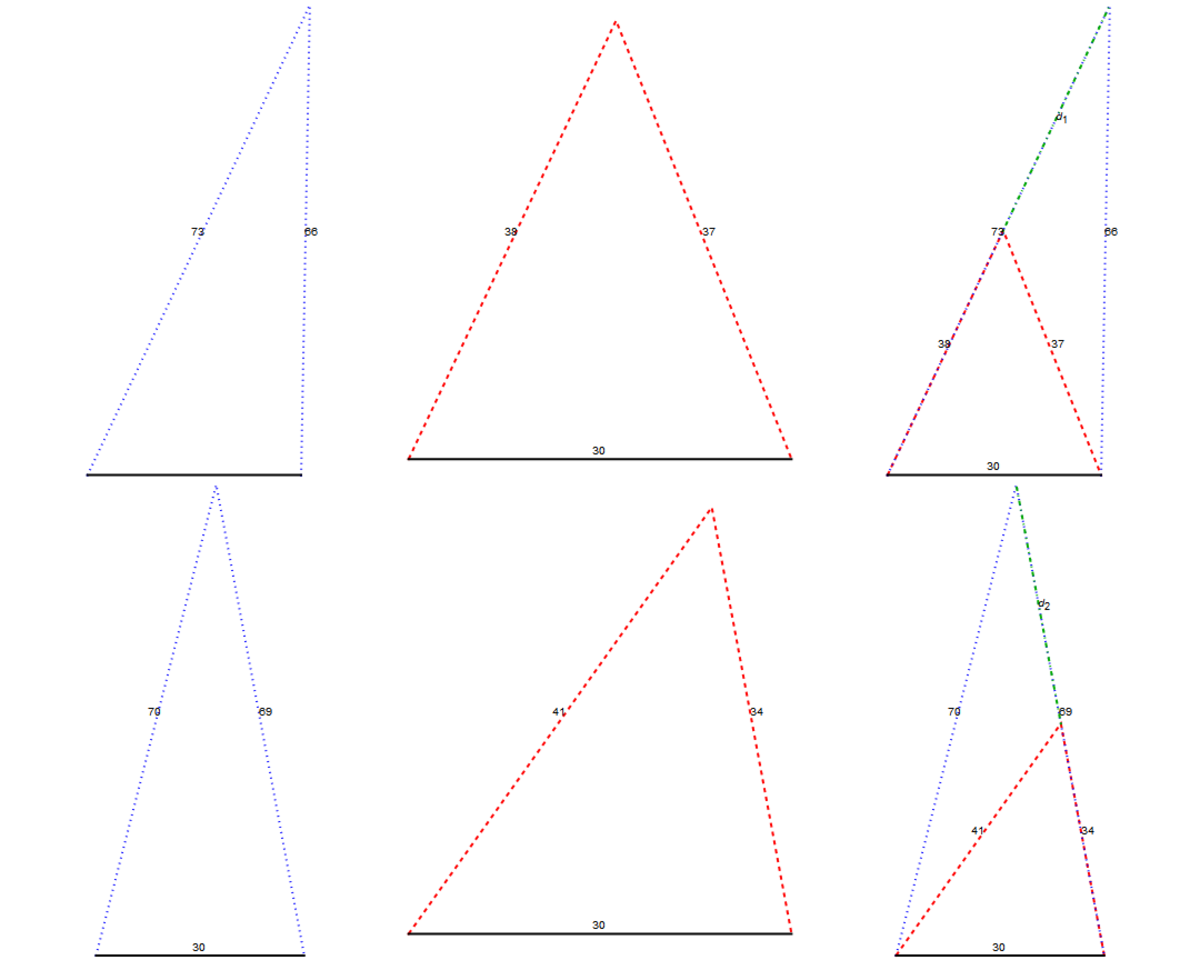
In case the numbers giving the side lengths of the triangles are hard to read in the images, here are they are in plain text: {{34, 41, 30}, {69, 70, 30}} and {{37, 38, 30}, {66, 73, 30}}.

The distance are reduced to their difference from the nearest integer, i.e., the distances are the Euclidean distances between the two triangles in each graphics. The triangles are placed so that each pair of triangles share a common, horizontal, (x)-axis base and that the third vertex of each triangle on the positive $y$ side of the $x$ -axis). I assumed that the left end of the base is at the origin. I found it simpler that way. The distances $d_n$ (the only reason for the subscripts on the $d_n$ values is to distinguish between the triangle pairs; there is no other operational purpose) are then reduced to their difference from the closest integer, i.e., $| d-[d]|$ where $|\cdots|$ means absolute value and $[\cdots]$ mean to round to the closest integer. No disambiguation rule should be necessary as the distances are very close to integers.

The answer is the absolute value of the reduced distances (themselves less than $10^{-7}$ ) multiplied by $10^{15}$ and rounded to an integer.

The answer is 0.

1 solution

A Former Brilliant Member
Oct 10, 2020

I did a brute force search of triangles with a horizontal base of length 30 and sides no greater than 99. I assumed that the left end of the base was at the origin and the triangle pair was positioned as described in the problem.

When I discovered that there were two sets of triangles with same reduced vertex distances, this problem arose. The common unreduced distance is $\frac{1}{2} \sqrt{\frac{13}{30} \left(53155-\sqrt{1751197161}\right)}\approx 35$ . The reduced distance is $1.75066*10^{-9}$ , which is even smaller than the reduced distance in the other problem.

For those of you who can read Wolfram Mathematica code:

triangleQ[a_, b_, c_] := AllTrue[{a, b, c, a + b - c, a + c - b, b + c - a}, #1 > 0 & ]

c = 30

t = Flatten[Table[If[triangleQ[a, b, c], {a, b, c}, Nothing], {a, 99}, {b, a, 99}], 1];


set = ParallelTable[v = (SSSTriangle @@ i)[[1,3]]; {i, Abs[v], N[Abs[v]]}, {i, t}]; 


small = Flatten[
  ParallelTable[z = EuclideanDistance[set[[i, 2]], set[[j, 2]]]; 
        y = Abs[z - Round[z]]; ny = N[y, 100]; 
   If[0 < ny < 2*^-8, {i, j}, Nothing], 
       {i, Length[set]}, {j, i + 1, Length[set]}], 1];


SortBy[Sort[({set[[#1[[1]],1]], set[[#1[[2]],1]], 
      -Subtract @@ MinMax[Transpose[{set[[#1[[1]],1]], set[[#1[[2]],1]]}][[1 ;; 2]]], 
      z = FullSimplify[EuclideanDistance[set[[#1[[1]],2]], set[[#1[[2]],2]]]]; 
       y = Abs[z - Round[z]]; z, N[y, 100]} & ) /@ small], #1[[5]] & ]

I've added the code formatting in your solution. But I can't seem to run it...

Apologies if I messed up your code by accident.

Pi Han Goh - 8 months ago

Your copy of the code seems valid. I was able to copy the code by cut-and-paste exactly, directly from the top, Mathematica box. Everything executed without problems and correctly.

small is {{45,1827},{66,1815},{113,1613},{119,2008},{132,1182},{136,2165},{140,1364},{167,1928},{178,1631},{215,2226},{219,1873},{245,1286},{272,1989},{293,1417},{303,2238},{323,2032},{333,1853},{393,1346},{443,810},{471,2157},{473,1713},{564,1337},{621,2049},{631,1287},{635,2154},{663,1230},{687,1231},{713,1368},{733,1782},{746,2223},{773,1817},{803,1934},{857,1733},{887,1853},{898,2213},{905,1563},{933,1535},{986,2280},{1023,1681},{1047,1824},{1051,1653},{1107,2000},{1178,1777},{1341,2183},{1347,1646},{1382,1801},{1463,1734},{1847,2158},{2081,2298}}

The line starting with SortBy also worked correctly in the same circumstances as above. The first two entries in the result from it are the basis of the basis of this problem. The beginnings of the two entries are {{34, 41, 30}, {69, 70, 30},...} and {{37, 38, 30}, {66, 73, 30},...}. If I were to give the remainders of the entries, then I would be disclosing the answer to the problem. The sides of the four triangle involved and are listed here though as those data are in the problem statement as well.

I have been using Mathematica InputForm rather than the more usual StandardForm as InputForm survives transmission through Brilliant.org much better.

The running of the code used 1.4GB on my computer, in additional to the Mathematica program's memory usage. This simply would not run on a Raspberry Pi machine with 2GB or less. It ought to run on a 4GB or 8GB Raspberry PI using Table instead of ParallelTable. I have no idea of what the execution time would be on a Raspberry PI. By the way, changing the ParallelTable symbols to Table symbol does not affect the final results and would not require multiple kernels, though that change did increase memory usage very slightly.

A Former Brilliant Member - 8 months ago

For Pi Han Goh and Chris Lewis, since you asked the question that led to this problem.

The answer is 0.

1 solution

0 pending reports