Apply Partial Fractions With Complex Numbers

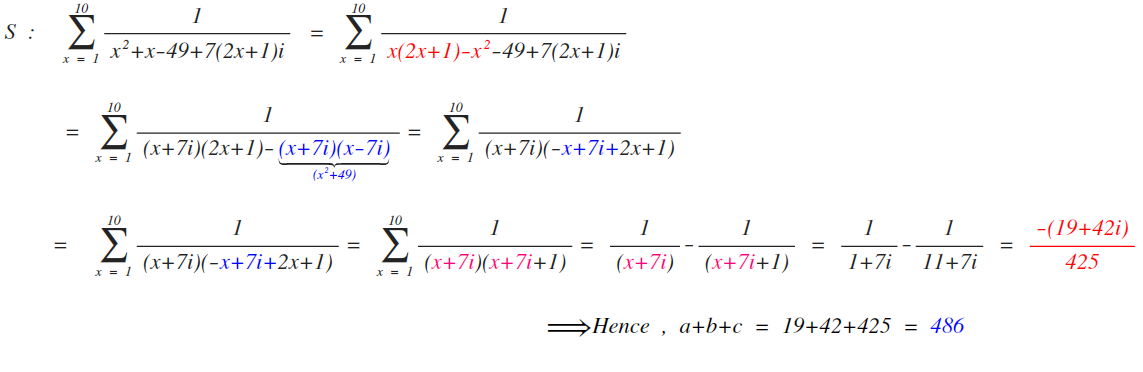
First let us try to factorize the denom. of the summation expression.

$x^2+x+(14x+7)i -49 \\ = x^2+x+14xi+7i-49 \\ = x^2+x+14xi+7i+i^249 \dots \because \ i^2=-1 \\ = x^2+x+7xi+7xi+7i+i^249 \\ = x(x+1+7i)+7i(x+1+7i) \\ = (x+7i)(x+1+7i)$

Now let us substitute this beautiful factorization in the summation expression:

$\sum_{x=1}^{10} \dfrac{1}{(x+7i)(x+1+7i)}$

Now this reduces to simple telescopic summation:

$\sum_{x=1}^{10} \dfrac{x+1+7i-(x+7i)}{(x+7i)(x+1+7i)} \\ = \sum_{x=1}^{10} \dfrac{1}{x+7i} - \dfrac{1}{x+1+7i} \\ = \dfrac{1}{1+7i}-\dfrac{1}{2+7i}+\dfrac{1}{2+7i}-\dfrac{1}{3+7i}+\dfrac{1}{3+7i}-\dots-\dfrac{1}{10+7i}+\dfrac{1}{10+7i}-\dfrac{1}{11+7i} \\ =\dfrac{1}{1+7i}-\dfrac{1}{11+7i} \\ \text{Multiplying numerator and denominator by the complex conjugate of the denominator , we get:} \\ =\dfrac{1-7i}{1^2+7^2} - \dfrac{11-7i}{11^2+7^2} \\ =\dfrac{1-7i}{5} - \dfrac{11-7i}{170} \\ = \dfrac{170-1190i-550+350i}{8500} \\=\dfrac{-380-840i}{8500} \\ = \boxed{\dfrac{-19-42i}{425}}$

Hence , $a+b+c=19+42+425=\boxed{486}$ .

remarkable question