For those who don't know part 2 (Determinants)
X = ∣ ∣ ∣ ∣ ∣ ∣ 0 3 5 1 5 7 2 5 5 ∣ ∣ ∣ ∣ ∣ ∣
Find the value of determinant ( X )
If you don't know how to expand determinants, look at this WIKI
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Or you can use the Sarrus' rule too. But, yeah, the general method is much more efficient and reliable. :D
We know that in calculating for determinant, the row operation r o w i − C ˙ r o w j will not change the value of the determinant. Therefore, we should do row operations to create more 0 's to ease the final calculation.
The following should that by making two zeros in a column calculation is much reduced. The row operation is r o w 2 − 5 3 r o w 3 → r o w 3 .
X = ∣ ∣ ∣ ∣ ∣ ∣ 0 3 5 1 5 7 2 5 5 ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ 0 0 5 1 0 . 8 7 2 2 5 ∣ ∣ ∣ ∣ ∣ ∣ = ( 1 ) ( 2 ) ( 5 ) − ( 2 ) ( 0 . 8 ) ( 5 ) = 1 0 − 8 = 2
If the elements were large, then this would've been a much more elegant way. But since the elements aren't much large values, we can simply expand along R 1 (or any other row/column one prefers) without using any properties of determinants.
sarrus rule can be used .so,
67-65=2
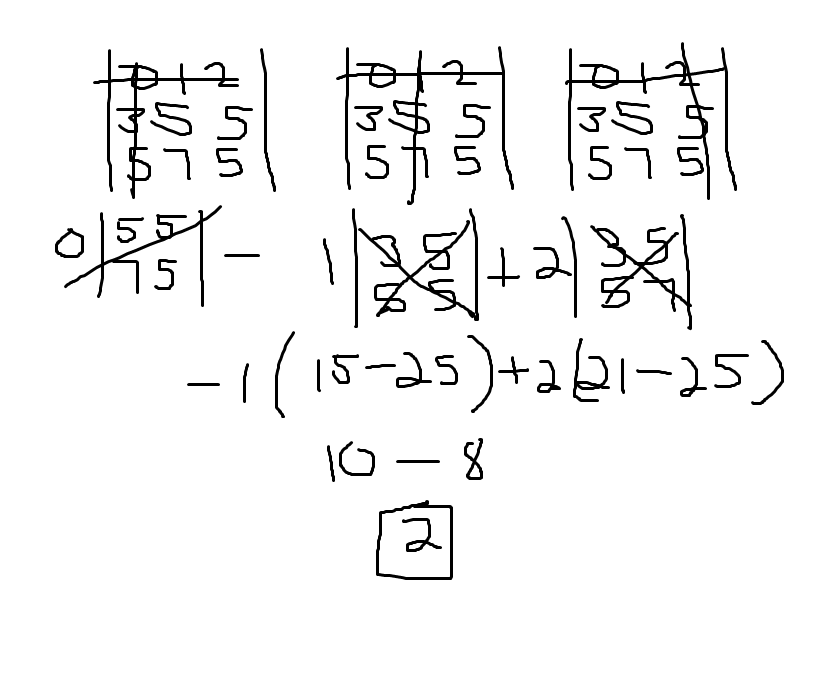
If you don't know how to expand determinants, look at this WIKI . X = ∣ ∣ ∣ ∣ ∣ ∣ 0 3 5 1 5 7 2 5 5 ∣ ∣ ∣ ∣ ∣ ∣ X = 0 × ∣ ∣ ∣ ∣ 5 7 5 5 ∣ ∣ ∣ ∣ − 1 × ∣ ∣ ∣ ∣ 3 5 5 5 ∣ ∣ ∣ ∣ + 2 × ∣ ∣ ∣ ∣ 3 5 5 7 ∣ ∣ ∣ ∣ X = 0 × ( ( 5 × 5 ) − ( 5 × 7 ) ) − 1 × ( ( 3 × 5 ) − ( 5 × 5 ) ) + 2 × ( ( 3 × 7 ) − ( 5 × 5 ) ) X = 0 + 1 0 − 8 X = 2