For those who don't know part 2 (omega)
( 9 ω 2 − 7 9 − 7 ω − 5 ω − 3 5 − 3 ω 2 ) 8 = ?
If you like this problem try to solve this
Details and Assumption
ω denotes the cube root unity ( = 1 )
The answer is 81.0000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
i also apply this steps...
Nice solution , stucked on 3rd line, +1
Note :the solution is the first two lines only the other paragraphs are only for more understanding.
Because ω is one of the cubic roots of 1 ∴ ω 3 = 1
X = ( 9 ω 2 − 7 9 − 7 ω − 5 ω − 3 5 − 3 ω 2 ) 8 = ( 9 ω 2 − 7 9 ω 3 − 7 ω − 5 ω − 3 5 ω 3 − 3 ω 2 ) 8 = ( 9 ω 2 − 7 ω ( 9 ω 2 − 7 ) − 5 ω − 3 ω 2 ( 5 ω − 3 ) ) 8 = ( ω − ω 2 ) 8 = ( ± 3 i ) 8 = 8 1 i 8 = 8 1
- For those who don't understand why ( ω − ω 2 ) = ± 3 i ω = 2 − 1 ± 3 i t h e n ω 2 = ( 2 − 1 ± 3 i ) 2 = 2 − 1 ∓ 3 i , so ( ω − ω 2 ) could be ( ω − ω 2 ) = ( 2 − 1 + 3 i ) − ( 2 − 1 − 3 i ) = 3 i or could be ( ω − ω 2 ) = ( 2 − 1 − 3 i ) − ( 2 − 1 + 3 i ) = − 3 i
∴ ( ω − ω 2 ) = ± 3 i
- For those who don't understand why ω = 2 − 1 ± 3 i and ω 2 = 2 − 1 ∓ 3 i
( copied from Kalpok Ethbrw solution )
X 3 = 1 or ( x − 1 ) ( x 2 + x + 1 ) = 0
Either x = 1 or, x 2 + x + 1 = 0 Then x = 2 . 1 − 1 ± − 1 2 − 4 . 1 . 1 or, x = 2 − 1 ± − 3 or, one root of x is 2 − 1 + 3 . i . This is called ω if we take ω 2 We will discover it is another root of the equation. The root is 2 − 1 − 3 . i .
Note : we can also take ω = 2 − 1 − 3 i then ω 2 = 2 − 1 + 3 i
∴ ω = 2 − 1 ± 3 i and ω 2 = 2 − 1 ∓ 3 i
Since ω and ω 2 are complex cubic roots of 1 :
⇒ ω 3 = 1 and ω 2 + ω + 1 = 0
Therefore,
X = ( 9 ω 2 − 7 9 − 7 ω − 5 ω − 3 5 − 3 ω 2 ) 8 = ( ω 2 ( 9 ω 2 − 7 ) 9 ω 2 − 7 ω 3 − ω ( 5 ω − 3 ) 5 ω − 3 ω 3 ) 8
= ( ω 2 ( 9 ω 2 − 7 ) 9 ω 2 − 7 − ω ( 5 ω − 3 ) 5 ω − 3 ) 8 = ( ω 2 1 − ω 1 ) 8
= ( ω 2 ω 3 − ω ω 3 ) 8 = ( ω − ω 2 ) 8 = ( ( ω − ω 2 ) 2 ) 4
= ( ω 2 − 2 ω 3 + ω 4 ) 4 = ( ω 2 − 2 + ω ) 4 = ( ω 2 + ω + 1 − 3 ) 4
= ( 0 − 3 ) 4 = 8 1
( 9 ω 2 − 7 9 − 7 ω − 5 ω − 3 5 − 3 ω 2 ) 8 M u l t i p l y i n g a n d d i v i d i n g ω i n t h e n u m e r a t o r a n d d e n o m i n a t o r o f b o t h t h e t e r m s . = ( ( ω ) ( ω ) 9 ω 2 − 7 ( ω ) 9 − 7 ω − 5 ω − 3 ( ω ) 5 − 3 ω 2 ( ω ) × ω 1 ) 8 = ( 9 ω 3 − 7 ω 9 − 7 ω ( ω ) − 5 ω − 3 5 ω − 3 ω 3 × ω 1 ) 8 B u t ω 3 = 1 , S o = ( 9 − 7 ω 9 − 7 ω ( ω ) − 5 ω − 3 5 ω − 3 × ω 1 ) 8 C a n c e l l i n g l i k e t e r m s , = ( ω − ω 1 ) 8 P u t t i n g ω a s 2 − 1 + 3 , = ( 2 − 1 + 3 − 2 − 1 + 3 1 ) 8 R a t i o n a l i z i n g t h e s e c o n d t e r m , w e g e t ω 1 = ω 2 = ( 2 − 1 + 3 − 2 − 1 − 3 ) 8 = ( − 2 1 + 2 3 + 2 1 + 2 3 ) 8 = ( 3 ) 8 = 8 1
Cheers!:)
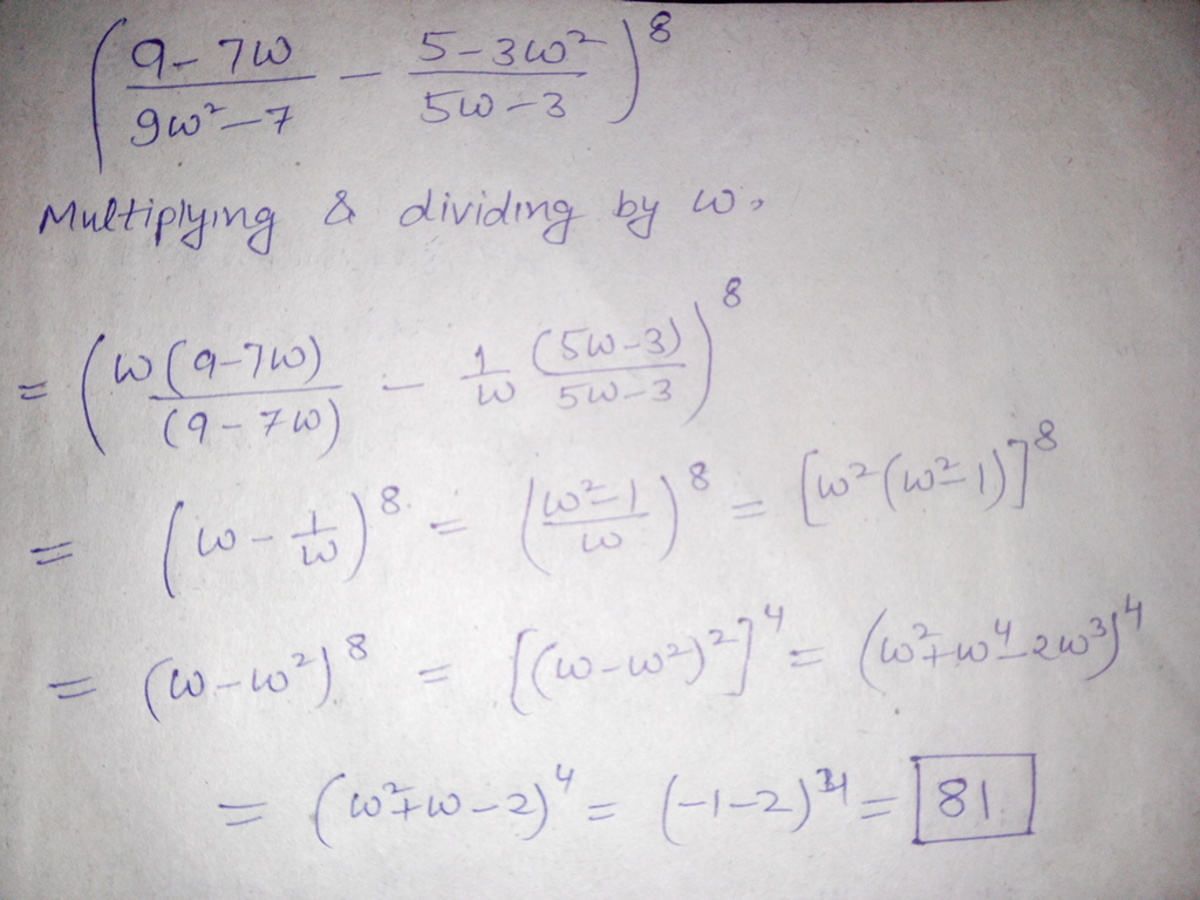
X = ( 9 ω 2 − 7 9 − 7 ω − 5 ω − 3 5 − 3 ω 2 ) 8
= ( ω 9 − 7 ω 9 − 7 ω − ω 2 5 − 3 ω 2 5 − 3 ω 2 ) 8
= ( ω − ω 2 ) 8
= [ ( ω − ω 2 ) 2 ] 4
= [ ω 2 + ω − 2 ] 4
= ( − 3 ) 4 = 8 1