For those who don't know part 3 (Determinants)
X = ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 1 2 − 1 2 2 7 4 2 4 5 − 6 1 2 2 3 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣
Find the value of det ( X ) .
If you don't know how to expand determinants, look at this wiki
Note: This problem isn't orginal.
The answer is -42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I am sorry for not mentioning the origin of the problem but I was deliberate to take the problem from khan academy because those who don't know how to solve 4 × 4 determinant understand the example well when they see the same problem is solved in the video , and the problem is just a practice for this NOTE
Log in to reply
Should at least mention the problem is not original.
Log in to reply
Sir,can I use your solution in my new Wiki ?
Sir, is it necessary that any 4 × 4 can be expressed as an upper (or lower) triangular matrix ?
- So, I tried solving this problem using Chió's method, to reduce the 4x4 matrix in a 3x3 one.
-
I have this picture, for those who don't even heard about this method/tool. It is simple, and it works in any 3x3 or bigger matrix.
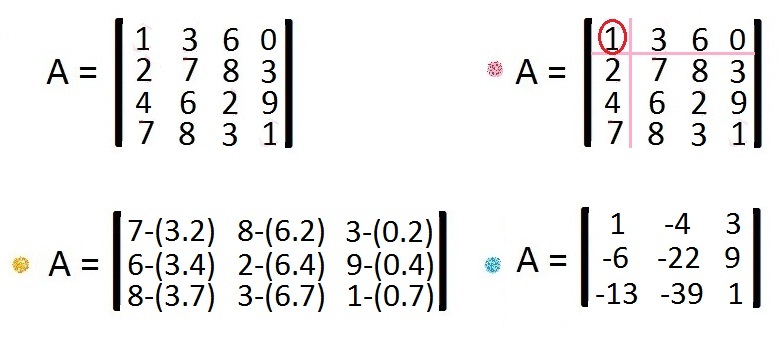
- After using Chió's, the matrix was reduced to:
- | 0 2 1 |
- | 3 1 0 |
- | 6 − 4 4 | ...(i'm sorry i'm not so skilled in writing solutions).
- Solving this matrix, we'll find out D e t = ( 0 + 0 − 1 2 ) − ( 6 + 2 4 + 0 ) = 4 2 .
My solution is by Expansion of Minors. I considered the first column. d e t X = ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 1 2 − 1 2 2 7 4 2 4 5 − 6 1 2 2 3 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 1 ∣ ∣ ∣ ∣ ∣ ∣ 2 7 4 4 5 − 6 2 2 3 2 7 4 4 5 − 6 ∣ ∣ ∣ ∣ ∣ ∣ − 1 ∣ ∣ ∣ ∣ ∣ ∣ 2 7 4 2 5 − 6 1 2 3 2 7 4 2 5 − 6 ∣ ∣ ∣ ∣ ∣ ∣ + 2 ∣ ∣ ∣ ∣ ∣ ∣ 2 2 4 2 4 − 6 1 2 3 2 2 4 2 4 − 6 ∣ ∣ ∣ ∣ ∣ ∣ + 1 ∣ ∣ ∣ ∣ ∣ ∣ 2 2 7 2 4 5 1 2 2 2 2 7 2 4 5 ∣ ∣ ∣ ∣ ∣ ∣
= 1 [ 3 0 + 3 2 − 8 4 − ( 4 0 − 2 4 + 8 4 ) ] − 1 [ 3 0 + 1 6 − 4 2 − ( 2 0 − 2 4 + 4 2 ) ] + 2 [ 2 4 + 1 6 − 1 2 − ( 1 6 − 2 4 + 1 2 ) ] + 1 [ 1 6 + 2 8 + 1 0 − ( 2 8 + 2 0 + 8 ) ]
= − 1 2 2 + 3 4 + 4 8 − 2
= − 4 2
After solving the problem, I noticed that the problem solution to this problem is given by this video clip from Khan Academy. Abdulrahman Khaled should give credit the originator of the problem and mentioned that the problem is not original.
Anyway, as mentioned in the video, the easy way to solve this to make the matrix into either an upper or lower triangular matrix with row operations and then the determinant is given by the product of the diagonal elements. Two row operation rules are involved.
I am showing another way of applying the same method here.
[ X ] = ⎣ ⎢ ⎢ ⎡ 1 1 2 − 1 2 2 7 4 2 4 5 − 6 1 2 2 3 ⎦ ⎥ ⎥ ⎤
r o w 1 → r o w 1 r o w 2 − 2 r o w 1 → r o w 2 r o w 3 − 2 r o w 1 → r o w 3 r o w 4 − 3 r o w 1 → r o w 4 ⇒ ⎣ ⎢ ⎢ ⎡ 1 − 1 0 − 4 2 − 2 3 − 2 2 0 1 − 1 2 1 0 0 0 ⎦ ⎥ ⎥ ⎤
r o w 1 → r o w 1 r o w 2 → r o w 2 r o w 3 → r o w 3 r o w 4 + 1 2 r o w 3 → r o w 4 ⇒ ⎣ ⎢ ⎢ ⎡ 1 − 1 0 − 4 2 − 2 3 3 4 2 0 1 0 1 0 0 0 ⎦ ⎥ ⎥ ⎤
r o w 1 → r o w 1 r o w 2 → r o w 2 r o w 3 → r o w 3 r o w 4 + 1 7 r o w 2 → r o w 4 ⇒ ⎣ ⎢ ⎢ ⎡ 1 − 1 0 − 2 1 2 − 2 3 0 2 0 1 0 1 0 0 0 ⎦ ⎥ ⎥ ⎤
r o w 4 → r o w 1 r o w 2 → r o w 2 r o w 3 → r o w 3 r o w 1 → r o w 4 ⇒ − ⎣ ⎢ ⎢ ⎡ − 2 1 − 1 0 1 0 − 2 3 2 0 0 1 2 0 0 0 1 ⎦ ⎥ ⎥ ⎤
Therefore, det [ X ] = X = − ( − 2 1 ) ( − 2 ) ( 1 ) ( 1 ) = − 4 2