Force of interaction between fast moving capacitor plates.
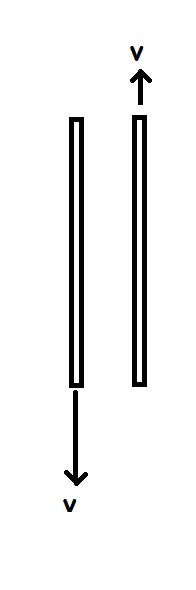 The plates of a
square
plate capacitor are separated by a
very small distance
and have charge
q
=
1
μ
C
side length
l
=
1
m
suddenly start moving in opposite directions with equal speed
v
=
2
×
1
0
8
m
/
s
as shown.
Find
the
force
experienced by one plate due to the other at this instant in
Newtons
.
The plates of a
square
plate capacitor are separated by a
very small distance
and have charge
q
=
1
μ
C
side length
l
=
1
m
suddenly start moving in opposite directions with equal speed
v
=
2
×
1
0
8
m
/
s
as shown.
Find
the
force
experienced by one plate due to the other at this instant in
Newtons
.
The answer is 0.0815.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I think fringing E field would also have significant effects.
Good question. I just think you could have written some assumptions, such as: consider the distance between the plates too small, don't consider the industion between them...
Interesting problem. I didn't get the correct answer because I had this intuition that moving plates (in sideways directions) would experience a lower force than if it were static. So I thought the answer was F = F E ( 1 − ( c v ) 2 ) .
wrong solution fringing forces cannot be neglected
Log in to reply
Hi, the distance between the plates is very small, and the fringing force would be negligible
Where am I going wrong? F = 2 L 2 ϵ 0 Q 2 ( 1 + c 2 v 2 ) F = 2 ( 1 ) 2 ( 8 . 8 5 4 × 1 0 − 1 2 ) 1 0 − 1 2 ( 1 + 9 × 1 0 1 6 4 × 1 0 1 6 ) F = 1 8 × 8 . 8 5 4 1 3 = 0 . 0 8 1 5
Log in to reply
I am also getting 0.081.. done exactly what you have done..!!
Dhruva Patil ; I am also getting the same answer as you.
Log in to reply
@Karan Siwach Guess they made some calculation error.
You are right . I am sorry for the inconvenience caused. It has been edited now. Thanks :)
Log in to reply
I think the answer was correct earlier-8.16 In the calculation above, length has been taken 1m while in question it is 0.1m which multiplies the answer by factor of 100, hence 8.16 . Did Exactly what you did but answer is 8.16 . Do please check and correct
length is 0.1m not 1m hence ans. must be 8.16
No consideration of relativity here? :P Just saying.
We know that the electric force between plates of a parallel plate capacitor is F E = 2 A ϵ 0 Q 2 = 2 L 2 ϵ 0 Q 2
Now, we know that motion of charges creates magnetic field. Now, due to the magnetic field due to motion of charges of left plate, charges of right plate will experience magnetic force.
Effective current flowing = i = d t d q = d t σ L d x = L Q v
Now, We use ampere's law to find magnetic field in region close to the plate.
Consider an amperian square loop of side x extending equally on both sides of left plate.
Clearly, B × 2 x = μ 0 i L x
⇒ B = 2 L 2 μ 0 Q v
Hence, F B = Q v B = 2 L 2 μ 0 Q 2 v 2 = F E c 2 v 2
Note that both the forces would be attracting. Hence, they add to each other.
Hence, , F = F E ( 1 + c 2 v 2 )
Put values to get the answer as 8 . 1 7
Note : it has been assumed that the distance between plates is very small. This is because the plates of a capacitor are very close to each other.