Play with matching square shape match sticks
Is it possible to form 3 identical squares with four matchsticks of length 1 and two of length 2 1 ?

Note : You are allowed to cross the matchsticks, but you are not allowed to break them.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
I don't think the second solution works, because there are parts that stick out (otherwise there would all sorts of solutions). And you mentioned why the first solution is flawed. Therefore, one could argue for no solutions.
Log in to reply
What you could do, is break each stick in half. This way the ratios between them stay the same, but you get rid of the heads. Now the shortened matches can be arranged as in the first part of this solution. Now we have three equal squares, no heads and no parts sticking out.
It never says that you can't have parts sticking out. The only requirement is to make 3 squares.
ah geez i thought the matches are not supposed to stack up
Log in to reply
I've added a note to specify that the matches can cross.
I also thought matches could not cross. That's how course's problems with matchsticks work
Log in to reply
I've added a note to specify that the matches can cross.
Well this is just stupid cause one "square" has no edges
Log in to reply
The goal is to make 3 squares. I included the grid so that the squares are easier to see.
Cool! I said not possible because I didn't have the sticks to try it out with. Can't believe I tricked myself into thinking I had to make four squares when trying to visualize the first solution!
But you are crossing the matchsticks. It specifically says you are not supposed to cross the matchsticks.
Log in to reply
The note says that you are allowed to cross the matchsticks.
I tried doing this with matchsticks but I couldn't figure it out. I think next time I should pay a bit more attention closely to the problem. I would rate this problem a 5 because I think it was in the middle of being easy and hard.
I thought it had to be yes. I didn't even try to figure it out... I kind of assumed that the first solution would work, but didn't think about it.
Little squares

Edit: ignore the colors. I should have made them all black as this method works with any six matchsticks.
Absolutely BRILLIANT, sir. You deserve a medal.
Smart. Great job for thinking outside of the ‘match’ box (get it? I know it’s terrible)
Log in to reply
Its incorrect.
This is my favorite solution! "Simple is never easy" :)
Wow! I wouldn't have thought of this!
This is absolutely great!
Why the colors? There are 4 long and 2 small. The colors point to 3 and 3.
Log in to reply
I drew it really fast in Paint and didn't notice I'd switch colors at the wrong time until after I uploaded it.
I don’t think its right actually. U added an extra long
4 long + 2 short?
I'm new to brilliant, but isn't this wrong? He used one matchstick more than he should.
This has 5 long and 2 short, its meant to be 4 long and 2 short
This method, however, could not ensure the side of 'squares' are even
The two short matchsticks just didn't come out looking like each other in this drawing, but it is understood what the intent is.
How are these squares identical?I mean since there is a square with 3 heads on its vertices and two with 2 heads.
If the origin (0,0) is the top left then point both 1/2" matchsticks towards (-x,-y). Point the exterior full 1" matchsticks towards origin. The intersecting matchsticks then would be pointed -x and negative -y respectively.
With that you have symmetry in each one having and identical corner two intersecting matchsticks.
It is a poorly worded question. It didn't specify whether you needed to use all the match sticks, or whether you could have loose ends. Without those stipulations the answer is an easy yes. With those it wood take some thought, but then the word identical comes into play with the match heads.
Here's my solution (black = length 1 and red = length 1/2):
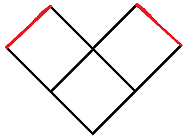
Nice diagram, and brilliantly short solution.
This is smart!
Some solutions are robotic...
Why can't we make 4 identical squares of 0.25 x 0.25?
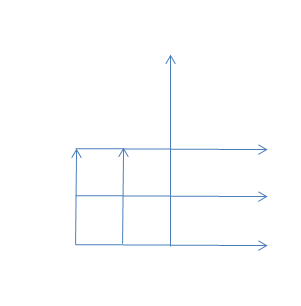
No, your diagram doesn't show three congruent squares being made. Adjust one of the arrows so that three congruent squares are made.
Stack the two small matches ontop of one another like a cross, then use four long sticks for the sides. Looking vertically downward you will see four indentical squares in the middle.
 Let the brown arrows be the matchsticks of length 1.
Let the green arrows be the matchsticks of length 1/2.
Let the brown arrows be the matchsticks of length 1.
Let the green arrows be the matchsticks of length 1/2.
if you do not care about the heads:
you can even make 4 squares:
Vli kllampa
Doesnt say you have to use all of the matchsticks. Its easy when you take away that restraint and also ends up with the correct conclusion according to the quiz.
Wrong. It does. The phrase "with four matchsticks of length 1 and two of length 1/2" means you are to use all six of them.
Square, not rectangle
Oops, I answered no because I thought it was four squares not three.
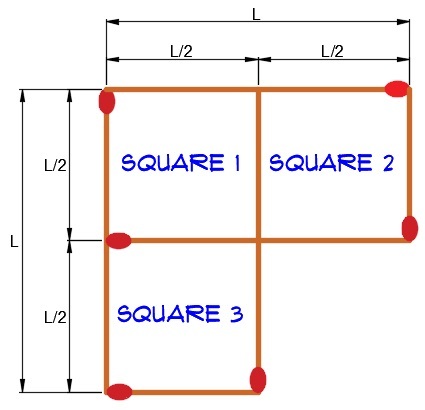
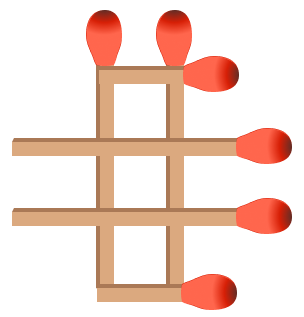
Here's a solution with 3 squares:
Now, you might be thinking, "What about the matchstick heads? Don't those make the squares not perfectly identical?" Here's a solution where the matchstick heads don't matter:
As you can see, you can even avoid the matchstick heads!