Forming a Team of Professionals
From ten people, how many ways can you form a team of eight people consisting of a project manager, two (equivalent) deputy project managers, and five (equivalent) engineers?
The answer is 7560.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Number of ways of picking 8 people from a group of 1 0 is, ( 8 1 0 ) = 4 5 Number of ways of picking 5 engineers from the above 8 people is, ( 5 8 ) = 5 6 Number of ways of picking 2 deputy project managers from the 3 people left is, ( 2 3 ) = 3 Number of ways of picking 1 project manager from the 1 person left is, ( 1 1 ) = 1 Therefore, the total ways of to form a team meeting the required conditions is, ( 8 1 0 ) ⋅ ( 5 8 ) ⋅ ( 2 3 ) ⋅ ( 1 1 ) = 4 5 ⋅ 5 6 ⋅ 3 ⋅ 1 = 7 5 6 0
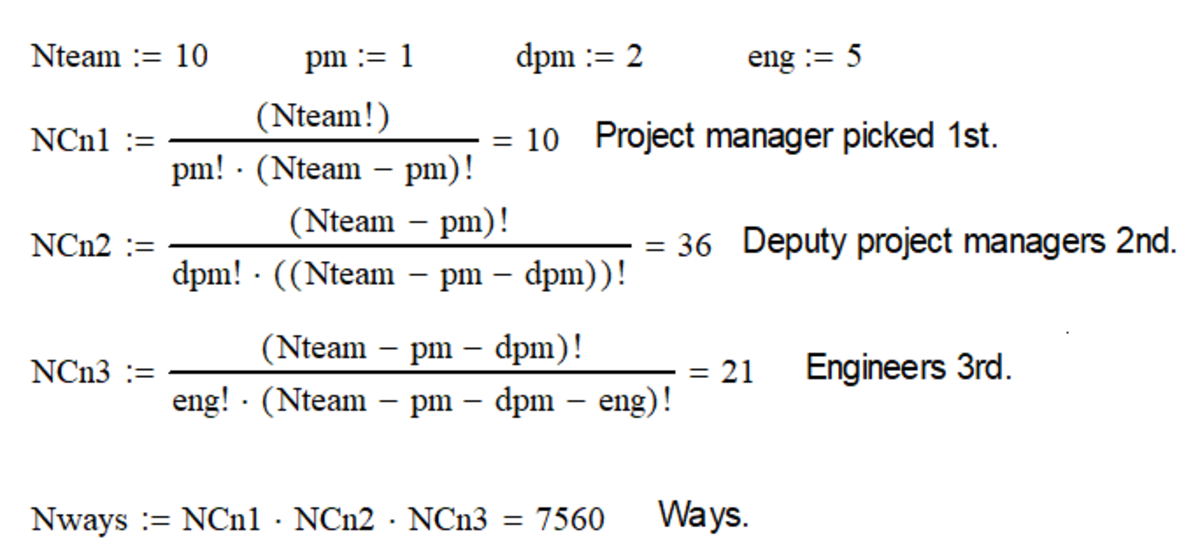
The project manager can be picked in 1 0 ways. The deputy project managers (indistinguishable) can be picked in 2 ! 9 × 8 ways, and by the same reasoning, the engineers can be chosen in 5 ! 7 × 6 × 5 × 4 × 3 ways.
In total, there are 1 0 × 2 ! 9 × 8 × 5 ! 7 × 6 × 5 × 4 × 3 = 7 5 6 0 ways to form the team.