Four Ball Collision
Four equal radii balls of masses 1kg, 2kg, 3kg, and 4kg as shown,
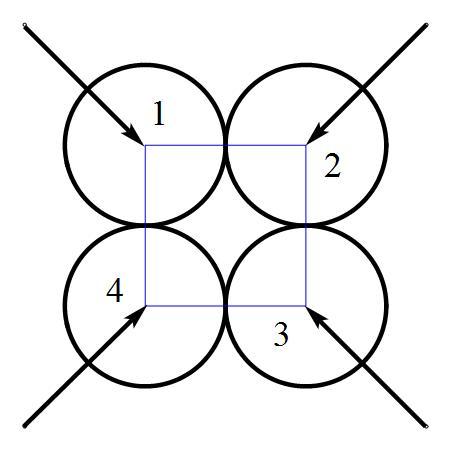
each moving with velocity 1 m/sec towards the same point P , collide at exactly the same instant. The points of contact form vertices of a square, the center of which is point P . When the balls fly apart after the collision, they move at velocities v 1 , v 2 , v 3 , v 4 .
If v 1 2 + v 2 2 + v 3 2 + v 4 2 can be expressed as B A , where A , B are coprime positive integers, then what is A + B ?
Assume collisions are ideal, i.e., perfectly elastic and frictionless.
The answer is 15713.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Very nice solution, saved me the effort of having to post one! I've added a note about the necessary conditions for an ideal collision, thanks for mentioning it. What's interesting is what happens with other multiple-ball collisions that doesn't neatly separate into orthogonal components.
Amazing problem! I had to study in some detail how to deal with multiple collisions before solving it. If you try and solve it considering pairs of collisions the result is wrong (my first try) and also depends on the chosen order of the collisions.
I did as follows. First of all, I used a reference frame where the x-axis lies on the 1-3 particles trajectory and the y-axis lies on the 2-4 particles trajectory. 1 and 4 travel in the positive x and y directions, respectively.
The problem now is that you have 8 unknowns (the eight components of the final four velocities, which we dub v 1 x , v 1 y , and so on) but only 3 equations, i.e. momentum conservation along x and y and energy conservation. We must take advantage of the fact that the collisions are simultaneous and happen with the geometry showed in the figure.
The main point is to use impulses. The impulse (Forces times time) is the momentum transferred in the instant of collision between two particles and it's orthogonal to the surface of contact. Let J 1 , J 2 , J 3 and J 4 be the moduli of the impulses between the pairs 12, 23, 34, 41, respectively.
Let the unit vectors normal to the contact surfaces be n ^ 1 = ( 2 / 2 , 2 / 2 ) , n ^ 2 = ( 2 / 2 , − 2 / 2 ) , n ^ 3 = ( 2 / 2 , 2 / 2 ) and n ^ 4 = ( 2 / 2 , − 2 / 2 ) .
Now we are ready. Let's call u , v , w and z the non-zero components of 1, 2, 3 and 4, respectively. Let's use momentum conservation along x: m 1 u = m 1 v 1 x + J 1 2 2 + J 4 2 2 , 0 = m 2 v 2 x − J 1 2 2 + J 2 2 2 , m 3 w = m 3 v 3 x − J 2 2 2 − J 3 2 2 , 0 = m 4 v 4 x − J 4 2 2 + J 3 2 2 . As it must be, the sum gives conservation of total momentum along x. Now, for y: 0 = m 1 v 1 y + J 1 2 2 − J 4 2 2 , m 2 v = m 2 v 2 y − J 1 2 2 − J 2 2 2 , 0 = m 3 v 3 y + J 2 2 2 − J 3 2 2 , m 4 z = m 4 v 4 y + J 4 2 2 + J 3 2 2 . Again, as it should be, the sum of the four equations reproduces the total momentum conservation along y.
Note that the problem can be generalized to whatever orientation of the collisions. What changes is that wherever you see 2 / 2 you would see a sine or cosine of the angle that the impulse form with the axis. Note also that we have now 8 equations, but twelve unknowns (we have also the impulses to deal with now). The situation has got better, thanks to the fact that the collisions are simultaneous and to our knowledge of their orientations. Now we need 4 more equations, which are provided by the energy conservation condition. Since the collisions are elastic the relative velocity is conserved in modulus along the direction of the collision. We can express this condition as follows: n ⋅ ( v 2 f − v 1 f ) = e n ⋅ ( v 1 i − v 2 i ) , where n is the unit vector normal to the collision surface and e is the restitution coefficient. The latter is 1 in our case, since the collisions are elastic. It would be zero for a totally inelastic collision or it can be left as a free parameter, thereby solving a more general problem.
For our four normal unit vectors given above, we have four elasticity conditions, which are the following: u − v = ( v 2 x − v 1 x ) + ( v 2 y − v 1 y ) , − w − v = ( v 3 x − v 2 x ) − ( v 3 y − v 2 y ) , − w + z = ( v 3 x − v 4 x ) + ( v 3 y − v 4 y ) , u + z = ( v 4 x − v 1 x ) − ( v 4 y − v 1 y ) . Note that the symmetry of the problem, i.e. the fact that cos ( π / 4 ) = sin ( π / 4 ) = 2 / 2 has helped a lot here because all the unit vectors components simplify. We must only take care of the correct signs.
We finally got our system of 12 equations for 12 unknowns. Now, let's use the data, i.e. we put u = z = 1 and v = w = − 1 and the values of the masses. The solution is: v 1 x = − 1 5 2 9 , v 2 x = − 1 5 8 , v 3 x = 3 5 3 3 , v 4 x = − 3 5 1 6 , v 1 y = 1 5 4 , v 2 y = 1 5 1 3 , v 3 y = 3 5 1 2 , v 4 y = − 3 5 9 , J 1 = 3 4 2 , J 2 = 5 1 2 2 , J 3 = 7 2 4 2 , J 4 = 5 8 2 . Calculating thus the sum of the square moduli, we get: v 1 2 + v 2 2 + v 3 2 + v 4 2 = 2 2 0 5 1 3 5 0 8 , and the answer to the question posed is 1 5 7 1 3 .
It's not a solution as elegant and as smart as Mark's one, but I hope it might be of some interest. I found very useful the following discussions:
http://physics.stackexchange.com/questions/173596/is-this-solveable-simultaneous-elastic-collision-of-4-objects-in-xy-plane
http://physics.stackexchange.com/questions/64130/how-multiple-objects-in-contact-are-resolved-in-an-inelastic-collision-when-edg/91069#91069
http://www.myphysicslab.com/Collision-methods.html
Grt problem and much better solution.hats off to your patience.I loved solving it.
We have to assume that all collisions between the balls are smooth and perfectly elastic . The collisions need to be smooth, so that horizontal and vertical (on the diagram) components can be handled separately, and they need to be perfectly elastic so that the coefficient of elasticity e = 1 . I guess the problem could be solved if we were told a different value of e , but the requirement for smoothness is crucial.
If two balls, one of mass u and another of mass v meet in a perfectly elastic collision travelling in a straight line, where the particle of mass u is travelling with velocity V and the particle of mass v is travelling with velocity − V , then the two particles will have velocities A u , v and B u , v respectively, where u A u , v + v B u , v = ( u − v ) V − A u , v + B u , v = 2 V using conservation of momentum and Newton's Law of Restitution with e = 1 . Thus A u , v = u + v u − 3 v V B u , v = u + v 3 u − v V . and hence A u , v 2 + B u , v 2 = ( u + v ) 2 1 0 u 2 − 1 2 u v + 1 0 v 2 V 2 = 2 V 2 [ 1 + 4 ( u + v u − v ) 2 ] Considering horizontal and vertical components, the ball of mass 1 has a horizontal collision with the ball of mass 3 , and also a vertical collision with the ball of mass 4 . The horizontal components of the mass 1 and mass 2 balls are equal and opposite (with V = 2 1 ), and the vertical components of the mass 1 and mass 4 balls are equal and opposite (with the same value of V . Thus the ball with mass 1 has velocity v 1 with horizontal component A 1 , 2 and vertical component A 1 , 4 , after the collision.
Arguing similarly for the other three balls , we deduce that v 2 has horizontal and vertical components B 1 , 2 and A 2 , 3 , that v 3 has horizontal and vertical components B 4 , 3 and B 2 , 3 , while v 4 has horizontal and vertical components A 4 , 3 and B 1 , 4 . Thus v 1 2 + v 2 2 + v 3 2 + v 4 2 = = = = A 1 , 2 2 + A 1 , 4 2 + B 1 , 2 2 + A 2 , 3 2 + B 4 , 3 2 + B 2 , 3 2 + A 4 , 3 2 + B 1 , 4 2 A 1 , 2 2 + B 1 , 2 2 + A 2 , 3 2 + B 2 , 3 2 + A 4 , 3 2 + B 4 , 3 2 + A 1 , 4 2 + B 1 , 4 2 4 [ 1 + ( 3 1 ) 2 + ( 5 1 ) 2 + ( 7 1 ) 2 + ( 5 3 ) 2 ] 2 2 0 5 1 3 5 0 8 making the answer 1 3 5 0 8 + 2 2 0 5 = 1 5 7 1 3 .