Four boats chasing
Four boats are on a large lake arranged so that they form the corners of a square of edge length ℓ = 1 km .
At time zero, each boat starts moving with velocity v boat = 1 0 k m / h such that its bow is always pointed directly toward its counterclockwise neighbor.
How long will the boats take to collide (in minutes)?
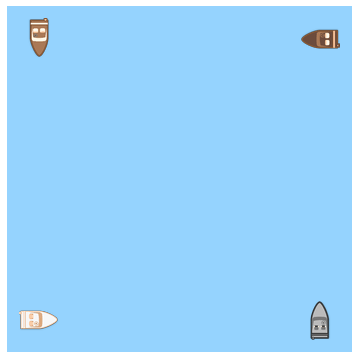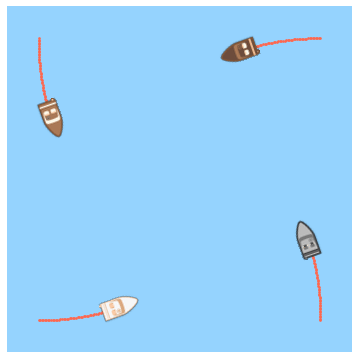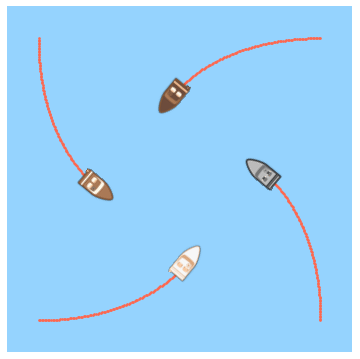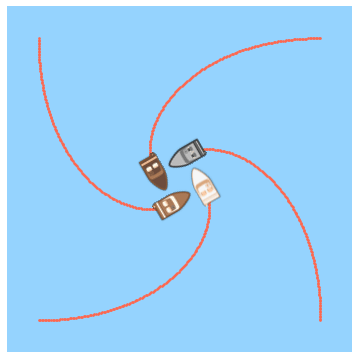
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
I love the appeal of your solution to symmetry and how much simpler it makes the problem :)
I also like this better than my solution.
Problem is not stated correctly. "It's bow is always pointed directly to its c.c.w neighbor" According to this when a boat starts it should move along the edge of the square, because that's the direction that points to its neighbor at start, and subsequently at all the time until it gets to the neighbor edge. This is not the path that is shown in the animation.
Log in to reply
In the animation each boat points directly to the neighboring boat at all times, as stated in the problem. It does not point to the neighboring vertex of the original square ; if that were the case, the boats would never meet, of course.
Log in to reply
Now it's correct. Problem should have stated "neighbor boat".
Imagine that you are in one of the boats. Let's look at the positions of your boat and your neighbor's boat (the one that you are chasing) at time t and t + Δ t . In the time Δ t your neighbor moved in the direction perpendicular to the straight line connecting the two of you, and accordingly, to the first order in Δ t , the distance between the two of you did not change. In other words your neighbor is neither getting away from your nor is he/her getting closer to you. On the other hand, you gain a distance of v Δ t , (where v is your velocity), because you are moving directly in his direction. (You also have to adjust the direction of your motion, so that at the time t + Δ t you are still aiming at your neighbor. However, adjusting the direction does not change the distance between the two of you.)
Since you are always gaining distance at the rate of your full velocity, and you neighbor's motion does not influence the distance between the two of you, you will have to travel exactly 1km to meet your neighbor. That will take 6 minutes.
Note: There is no need to determine the orbit. A similar argument (but a bit more complex geometry) works for any number of boats on the corners of a regular polygon.
"Note: There is no need to determine the orbit. A similar argument (but a bit more complex geometry) works for any number of boats on the corners of a regular polygon."
I don't think your statement above is true. The case of 4 boats on a square, is a very special case. The boat you are chasing, has motion perpendicular to your velocity and that motion to first order neither adds nor subtracts anything to the distance between you. The total distance you travel is still the original separation distance. The time it takes is still t = S/V.
A case with 3 boats in an equilateral triangle, the distance you travel before collision is LESS than the original distance. You can spreadsheet this, or program it or solve analytically. So the time is less than 6 minutes.
The degenerate case with N=2 is quite obviously less time. T = 3 minutes then.
The opposite case where N > 4, the boats will take longer than 6 minutes. For N>> 4 they will take very long indeed.
For example, the radius of the earth is about 4000 miles the circumference is about 25,000 miles. Imagine you had 25,000 boats arranged in a "circle" 1 mile apart. traveling 10 miles per hour. They would take at least 400 hours to reach the center of the circle where they would all collide. Actually, they'd take much longer as One Top says "Hence the time taken to converge = A/{v[1- cos(360°/n)]} in the general case." which is 31.66 million hours.
Log in to reply
You are perfectly right about the distances and times for the more general cases (2 boats, 3 boats, 5 boats e.t.c). However, I never argued that the result is as simple as the 4 boat situation. My argument was about getting the result without determining the orbit.
Here is for 3 boats: Consider a small amount of time Delta T. Boat #1 chasing boat #2 and gains a distance of v Delta t. (with its full velocity). Boat #2, while going after boat #3, also moves closer to boat #1 by a distance of v sin 30^o Delta t. (That is what I meant by " a bit more complex geometry". ) They always remain on the corners of an equilateral triangle and this argument will work every moment in time, The resultant time is t= a/[v(a+sin 30^o)].
It couldn't seem to work up a great intuition for this problem, so here's how I did it. Consider the initial conditions:
( x 1 , y 1 ) = ( 0 , 0 ) ( x 2 , y 2 ) = ( D , 0 ) ( v x 1 , v y 1 ) = ( v , 0 ) ( v x 2 , v y 2 ) = ( 0 , v )
After the first increment:
( x 1 , y 1 ) = ( v Δ t , 0 ) ( x 2 , y 2 ) = ( D , v Δ t )
The original distance was D . The new distance is (neglecting square infinitesimals):
D ′ 2 = ( D − v Δ t ) 2 + ( v Δ t ) 2 ≈ D 2 − 2 v D Δ t D ′ = D 2 − 2 v D Δ t
So we have a relationship between the distances at the present iteration and the previous iteration. Running this on a computer (with the original distance set to 1) and incrementing the time gives a final time of very nearly 6 minutes. Also, here's a plot of the spiral trajectory (made with an alternate program which calculates the 2D velocities at each time step using the 2D geometry).
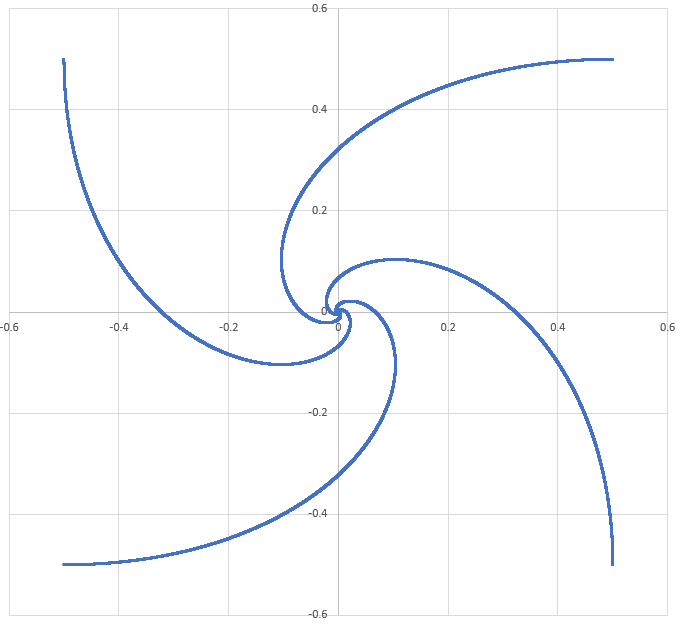
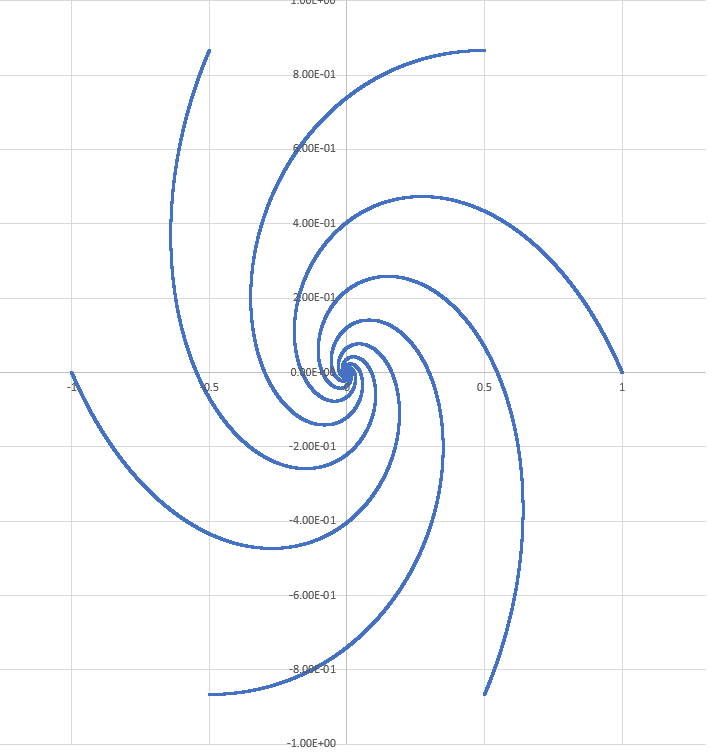
Here is what it looks like when you start with a unit-hexagon (6 boats).
If you expand the square root in your expression for D' in the limit of \Delta t -> 0, you will get D'=D-v \Delta t. This is exactly what I stated in my solution in a less mathematical form.
Excellent spirals!
Log in to reply
Oh, yes, I see. So it does end up being equivalent to yours.
1-2=0+3=3-4=0+5 etc
If you can do this for N= 3 and N = { 5, 6, 7, 8, 9, ... } you will get a set of pretty graphs and the dependence of collision time on the number of boats. It will be shorter for N=3 and longer for N > 4.
I thought of the boats as points on the complex plane, where each boat was moving towards a 90 degree rotation of it's current position, which gave the differential equation d t d x = i x − x x ( 0 ) = 0 . 5 + 0 . 5 i where x ( 0 ) was given for the top right boat, with solution x ( t ) = ( 0 . 5 + 0 . 5 i ) e ( − 1 + i ) t I then evaluated the path length to obtain the answer ∫ 0 ∞ ∣ − e ( − 1 + i ) t ∣ d t = ∫ 0 ∞ e − t d t = 1 k m 1 0 k m / h 1 k m = 6 m i n u t e s
At first I was very surprised that this approach works, because that ODE models that the boats slow down as they get closer to each other. However, as clarified in another comment, the ODE still gives the shape of the path taken. Thanks for the cool solution!
Interesting approach using complex numbers! This is new to me, could you explain how you obtained the differential equation d t d x = i x − x ?
Log in to reply
I noticed that at their initial positions each boat was a 90 degree counterclockwise rotation of its neighbor, and by symmetry would stay that way. Multiplying by i represents a 90 degree rotation on the complex plane, so ix-x "points" from one boat to its neighbor. This quantity doesn't represent the actual rate the boats are moving, but is great for answering how far each boat travels before meeting.
Consider any boat. It starts off at a distance of 1 km from its counterclockwise neighbour and travels directly towards it at a constant speed of 10 km/h and so takes 1/10th of an hour or 6 minutes to reach it.
Nice, finding the rate of change of distance between two boats to find the time makes the calculations very simple.
Suppose we have a regular n-gon of side A met. with a boat placed at each vertex and each boat moving exactly as stated in the problem. We find that with each move made simultaneously by the boats, the shape of the n-gon is maintained but its size goes on shrinking.
The distance to be covered = A and the relative velocity of any two boats near each other = v − v × cos n 3 6 0 ∘ by compounding velocities. Hence the time taken to converge = v ( 1 − cos n 3 6 0 ∘ ) A in the general case. In our case, n=4 so t = v ( 1 − cos 4 3 6 0 ∘ ) A = 1/(10) hr. = 6 min.
It is interesting how we can generalize the problem for n boats.
The velocity vector towards the centre is always constant at 2 1 km/hr. Distance b/w starting and the centre point is 2 1 0 and hence the solution. Apply Time equals Displacement/velocity.
Furthur to elaborate this is true because at any instant if we connect the boats we will have a square and all these squares have the same center.
I calculated the length of the spiral that the boat makes towards the center. I did that through geometrical series. In step dt the boat travels distance "a" along 1km edge of the initial square.
In the second step it travels distance a(1-a) of the rotated nested square.
In the next step dt it travels a ( 1 − a ) 2 and so on. It forms a geometrical series with a1=a and q= 1-a with the infinite sum for dt->0 of S=1km. Having v=10km/h and s=1km the time is 6 minutes.
Could you explain why the ratio of the geometric series is ( 1 − a ) ?
Simple solution
Due to symmetry, the positions of the four boats at any time t will be the vertices of a square. Let s be the side of that square. Since each boat is always moving exactly parallel to its side of the square, we have d t d s = − d t d x = − v . The boats meet when s = s 0 − v t = 0 . Therefore t = v s 0 = 1 0 k m / h 1 k m = 0 . 1 h r = 6 m i n .
Alternative solution
Consider the center of the lake the origin of a coordinate system ( 0 , 0 ) . Use polar coordinates: the position of boat 1 is ( r cos θ , r sin θ ) , where r and θ are functions of the time t . The position of boat 2 is ( r cos ( θ − 9 0 ∘ ) , r sin ( θ − 9 0 ∘ ) ) = ( r sin θ , − r cos θ ) .
The vector from boat 1 to boat 2 is therefore d = r ( sin θ − cos θ , − sin θ − cos θ ) . and as boat 1 is traveling in that direction at speed v , its velocity is v = d v d = 2 v ( sin θ − cos θ , − sin θ − cos θ ) . Splitting this in a radial and tangential component, we get v = v r a d + v t a n = − 2 v ( cos θ , sin θ ) − 2 v ( − sin θ , cos θ ) . The radial component gives the change in r , and the tangential component the change in θ : d t d r = − 2 v , d t d θ = − 2 r v . Solving the first of these equations with r 0 = 1 / 2 and v = 1 0 we get r t = 2 1 ( 1 − 1 0 t ) ; we see that r t = 0 when t = 1 / 1 0 hours, or 6 minutes.
The second equation becomes d t d θ = − 1 − 1 0 t 1 0 , θ t = θ 0 + ln ( 1 − 1 0 t ) . This value tends to − ∞ as t → 1 / 1 0 : the boats circle each other infinitely many times before actually meeting! Each boat will have completed a full revolution when ln ( 1 − 1 0 t ) = − 2 π t = 1 0 1 − e − 2 π ≈ 0 . 0 9 9 8 1 hours , that is, 99.8% of the total way.