Four bugs on a tetrahedron
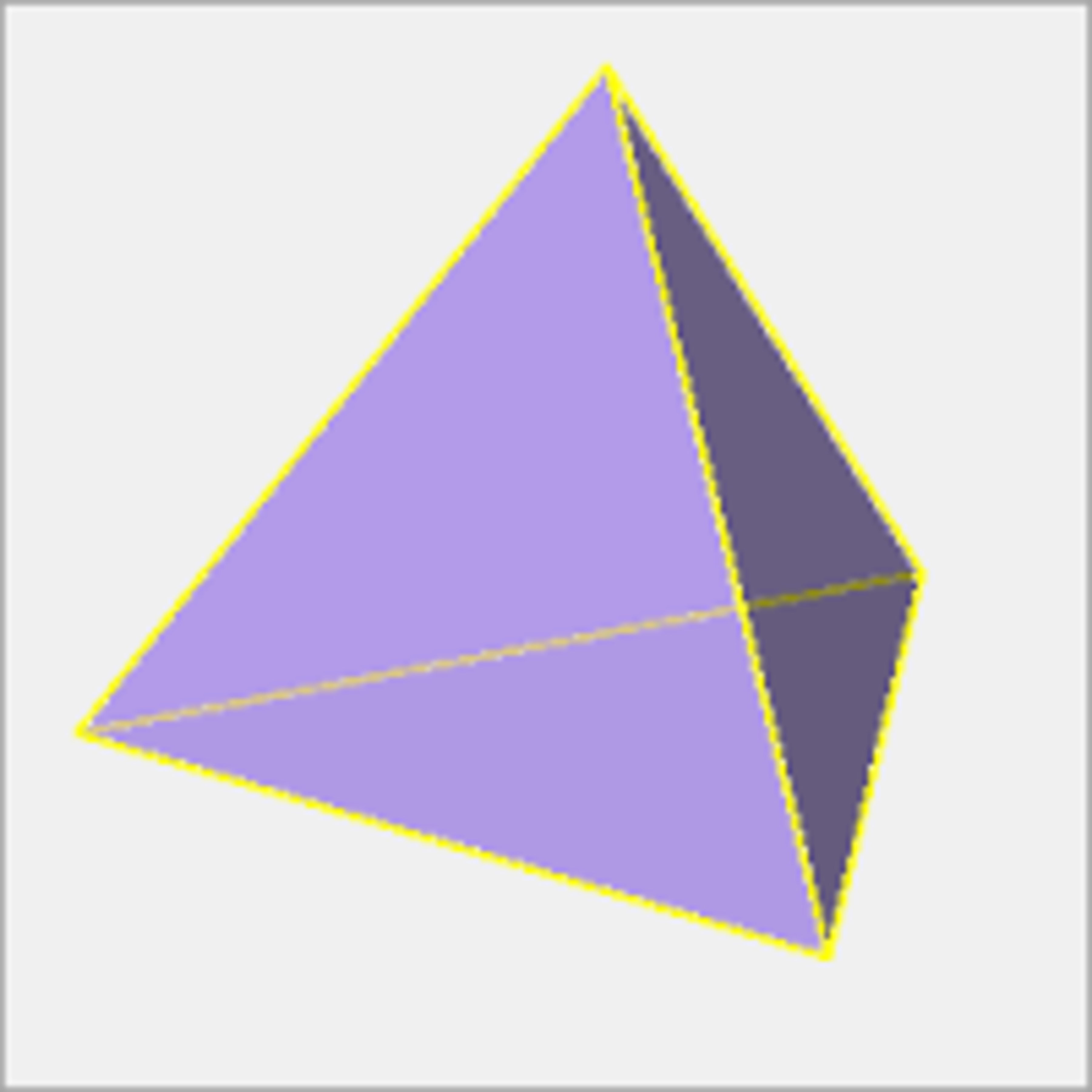
Four bugs start on the four vertices of a tetrahedron. They each randomly walk along one of the three edges available to them. What is the probability that no bug meets on an edge or a vertex?
If the answer is , where and are coprime positive integers, what is ?
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The number of ways the bugs can move is 3 ⋅ 3 ⋅ 3 ⋅ 3 = 8 1 , since each can choose from 3 available edges.
In order to not meet on either an edge or a vertex, implies that they move in a cyclic manner. e.g. A goes toward B , B goes toward C , C goes toward D , and D goes toward A .
There are only six ways to do this:
Therefore, the probability is 8 1 6 = 2 7 2
2 + 2 7 = 2 9