Four Circles and an Ellipse
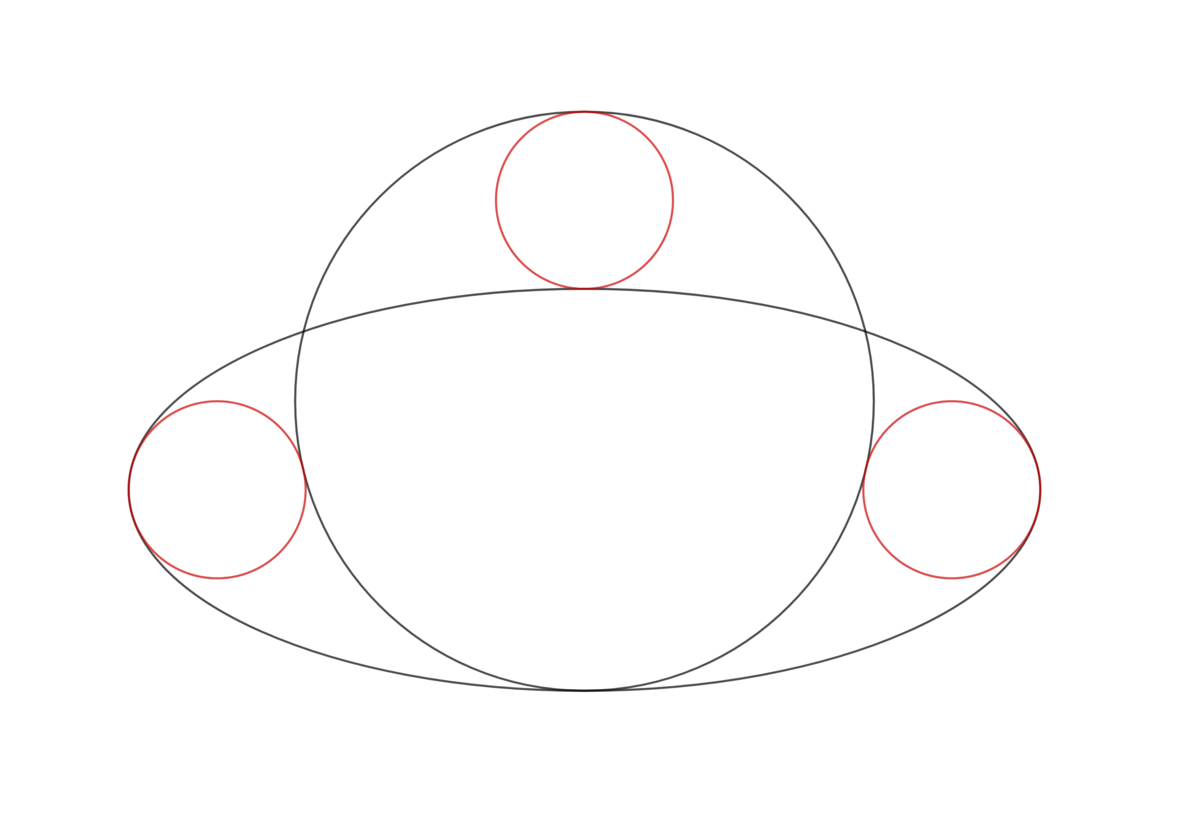
The figure shows four circles and an ellipse. They are tangent where the figure shows them to be. The three red circles are congruent and touch the ellipse at exactly one point. What is the greatest possible eccentricity e of the ellipse? Submit ⌊ 1 0 5 e ⌋ .
Inspiration here
The answer is 89769.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Without loss of generality, we can take the radius of the big black circle to be 1 . We'll also take the radius of the red circles to be r . If the ellipse has a semi-major axis a , and semi-minor axis b , then by summing the distances vertically, we get 2 = 2 r + 2 b , i.e. r + b = 1 . Taking the origin of the Cartesian reference frame to be at the center of the ellipse, then the center of the red circle on the right is ( a − r , 0 ) , and the center of the big black circle is at ( 0 , 1 − b ) . Hence, by the distance formula applied to these two centers,
( 1 + r ) 2 = ( a − r ) 2 + ( 1 − b ) 2
Substituing r = 1 − b , this becomes,
( 2 − b ) 2 = ( a + b − 1 ) 2 + ( 1 − b ) 2
Expanding, and simplifying,
a 2 + b 2 + 2 a b − 2 a − 2 = 0 ( 1 )
This equation has many solutions for a and b . However, if we make an additional constraint on the small red circle, then we can find a unique solution. That constraint, which is not mentioned but implied in the supplied diagram, is that the red circles at the right and left have the same curvature as the ellipse at the points to tangency.
The radius of curvature of the ellipse a 2 x 2 + b 2 y 2 = 1 at the point ( a , 0 ) is given by ρ = a b 2 . This can be deduced by using the parameteric equation of the ellipse, which is p ( t ) = ( a cos t , b sin t ) , and using the formula for the radius of curvature, at t = 0 ,
ρ ( t ) = ∣ p ˙ ( t ) ∣ 2 ∣ p ¨ ( t ) ∣ 2 − ( p ˙ ( t ) ⋅ p ¨ ( t ) ) 2 ∣ p ˙ ( t ) ∣ 3
Thus, we'll set r = ρ , so that 1 − b = a b 2 which re-arranges to,
b 2 + a b − a = 0 ( 2 )
Solving equations ( 1 ) , ( 2 ) results in
a = 1 . 5 7 5 3 8 5 1 2 2
b = 0 . 6 9 4 1 4 5 7 2 1
Therefore, the eccentricity is e = 1 − ( b a ) 2 = 0 . 8 9 7 6 9 3 8 6 7
And the answer is ⌊ 1 0 5 ( 0 . 8 9 7 6 9 3 8 6 7 ) ⌋ = 8 9 7 6 9
As my solution shows, you can have a diagram of the required type for any positive eccentricity less than the critical value. The requirement of equal radius of curvature for the red circles and the ellipse it not necessary for the diagram to exist (although it is true in the critical case, since that is the changeover point between the red circles being internally and externally tangent at the end of the semimajor axis); what is key is the ability to have an inscribed circle that is tangent at the end of the semi-major axis.
Hosam, Wolfram gets a different solution to equations (1) and (2).
Oh it's just a typo. (1) should be a 2 + b 2 + 2 a b − 2 a − 2 = 0
Log in to reply
Thanks for pointing it out. I've updated my solution.
There are infinitely many possible values of the eccentricity.
If r is the radius of the red circles, then the radius of the larger circle is r + b . Then we must have a = ( 2 r + b ) sin θ + r where cos θ = 2 r + b r , so we deduce that ( a − r ) 2 2 r 2 + 2 ( a + 2 b ) r [ r + 2 1 ( a + 2 b ) ] 2 r = ( 2 r + b ) 2 sin 2 θ = ( 2 r + b ) 2 − r 2 = a 2 − b 2 = 4 1 ( 3 a 2 + 4 a b + 2 b 2 ) = 2 1 [ 3 a 2 + 4 a b + 2 b 2 − a − 2 b ] We must have r > 0 , which requires a > b and hence e > 0 . Here are a couple of examples, showing that different values of the eccentricity are indeed possible:
There is an upper limit on the possible values of e . As shown here , there is a limit on the position of the centre of the two circles on the major axis that enables the circles to be tangent to the ellipse at the single point at the end of the semimajor axis, and also be inscribed inside the ellipse. This condition is that a − r ≥ a e 2 , which means that ξ = 1 − e 2 must satisfy the inequality 2 ξ 4 + 4 ξ 3 + 3 ξ 2 − 1 ≥ 0 for 0 < ξ < 1 , which means that 1 > ξ ≥ 0 . 4 4 0 6 1 9 7 0 0 5 , which in turn implies that 0 < e ≤ 0 . 8 9 7 6 9 3 8 6 7 4 . Thus this construction is possible provided that 0 < e ≤ 0 . 8 9 7 6 9 3 8 6 7 4 . Here is another picture showing what goes wrong if e is too big:
Thus e ^ = 0 . 8 9 7 6 9 3 8 6 7 4 is the critical value of e , and so the answer is ⌊ 1 0 5 e ^ ⌋ = 8 9 7 6 9 .