Four Circles In A Parallelogram
Four circles are inscribed in a parallelogram as in this figure:
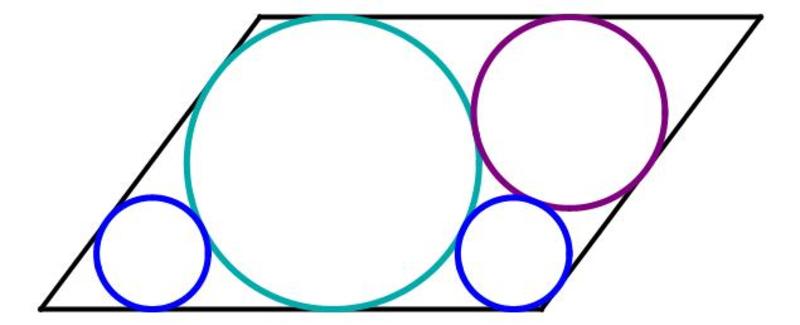
The two smallest circles have the same radius.
If θ is the acute angle of the parallelogram, then tan θ can be expressed as a fraction b a , where a and b are positive coprime integers. Find the sum a + b .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thanks for posting a solution!
Fourth line of the equation F H . Should it not be FA? Even in next line.
Thanks for the catch, Niranjan. Fixed.
this took me way too much so I just gave up. I'm only 15 tho, so can I consider that an excuse?
Another nice problem by Mr. Mendrin! For reference, if the radius of the large circle is 1, then the radius of the two smaller blue circles is 2 3 − 5 , and the radius of the purple circle is 8 3 + 5 .
I tried solving the problem properly, but quickly got bogged down in the calculations. I then resorted to adjusting the variables, until the diagram looked right, and guessed. Perhaps Mr. Mendrin can furnish a good solution.
Okay, I'll post a solution later this week, Jon. Let's see how short I can make it.
I thought of slope or Tan(half of acute angle) =(1/2) which fits into the scheme. Therefore, Answer=4/3, Formal answer gets you in few triangular and algebraic relations. Did a geometric construction to verify.
In the following figure, circles with centers A , Z have the same radius a , circle with center B has radius b , and circle with center C has radius c . We'll assume that a = 1 for simplification.
First:
D A = ( ( c + a ) 2 − ( c − a ) 2 = 2 a c
E B = ( ( c + b ) 2 − ( c − b ) 2 = 2 a b
F B = E B − D A
F A = 2 c − a − b
F B 2 + F A 2 = a + b
which gets us
c = 2 a b
Solving for b , we have
b = 4 a c 2
Now, all of the following triangles are similar:
Δ C D Z
Δ Z H G
Δ K J C
Δ B N Q
Δ L M A
where
Z D C D = 2 a c c − a = T a n ( θ ) = C o t ( θ ) 1
Because G K = L Q , we have
a C o t ( θ ) + 2 a c + c T a n ( θ ) = a T a n ( θ ) + 2 a b + b C o t ( θ )
Letting a = 1 and b = 4 c 2 , and eliminating the denominator, we're left with
2 c 2 c − c 2 − 2 c c − 3 c + 1 = 0
Letting c = d 2 , we have
2 d 5 − d 4 − 2 d 3 − 3 d 2 + 1 = 0
which factors into
( 2 d − 1 ) ( d 2 + d + 1 ) ( d 2 − d − 1 ) = 0
which has only one real solution where d > 1
d = 2 1 ( 1 + 5 )
c = d 2 = 2 1 ( 3 + 5 )
Since
T a n ( θ ) = 2 a c c − a
we can let a = 1 , and find the tangent of twice the angle
T a n ( 2 A r c T a n ( 2 a c c − a ) ) = 3 4