Four coins

Logic Level 3

There are four coins arranged as such:

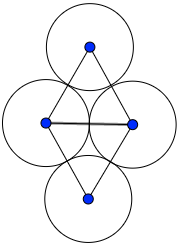
Note: The rhombus created by the centers of the circles is comprised of two equilateral triangles.

A move is defined to be moving a coin to another location such that at the end of the move, the coin that was moved is touching two other coins. Hence, how many moves are needed in order to obtain 4 coins in a straight line, like this? The orientation of the coins does not matter, the only condition is that their centers lie on one line.

Enter -1 if it is impossible to do so. Bonus: Prove it!

The answer is 4.

1 solution

Andrew Ellinor
Jan 29, 2016

A total of four moves is required:

Hi I typed in 2 because I moved the top circle in between the two middle ones which makes an almost straight line and then I put the bottom circle in the middle of the 3 circles. Why isn't that valid? (Also as a side note when I got my first answer 2 wrong, I was about to say it was impossible to do because the picture of the end result is a horizontal line, which isn't possible to achieve. I thought the question was vague in terms of what kind of line was acceptable.)

P L - 5 years, 4 months ago

That is not valid because on placing the upper circle in between the two middle ones you are also moving the middle circles which means that at the end of the first step the middle circles should also be in contact with two other circles

Sanjeev Gupta - 5 years, 4 months ago

Thanks a lot for that, I was really confused why that wasn't valid either. :)

Drex Beckman - 5 years, 4 months ago

Thanks for the reply

P L - 5 years, 4 months ago

Took me a minute to figure this out

Chris Ruggieri - 5 years ago

I did in it reverse: how many steps to go from the straight line to the rhombus, if the condition is that a moved coin must have been touching two just prior to being moved.

Peter Byers - 4 years, 4 months ago

The correct answer is TWO -move 2 to the bottom of 4- slide 3 between1 and 4- done

Don Ford - 2 years, 5 months ago

Four coins

The answer is 4.

1 solution

0 pending reports