Four color fun
The four color theorem says no map requires more than four colors, but some can require fewer.
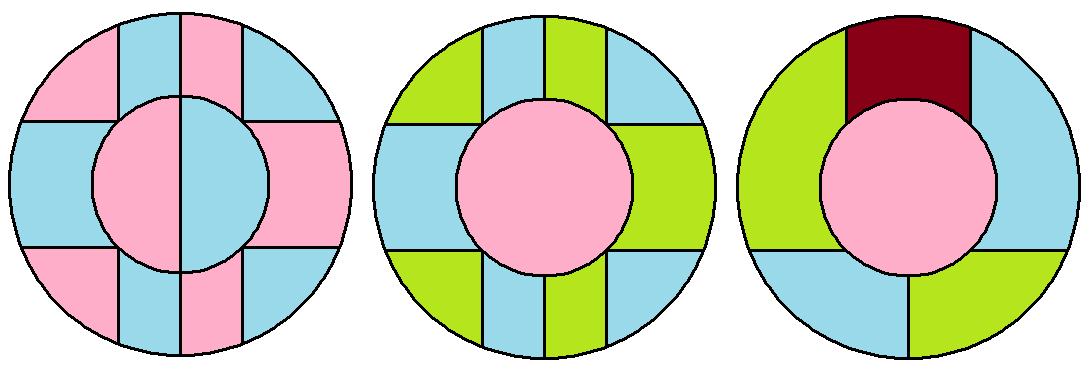
- The first illustration shows a 12-region map that only requires two colors.
- In the second illustration, you erase a boundary to create an 11-region map that requires three colors.
- In the last, you erase 5 more boundaries to create a 6-region map that requires four colors.
Begin with a map that can be two-colored.
Erase one or more boundaries to create a new map that requires three colors.
Again erase one or more boundaries to create a final map that requires four colors.
What is the minimum number of regions in the starting map for this to be possible?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A lower bound on the answer is 6. This is possible if only one border is erased each time. Here is one solution that does achieve 6 .