Four Equals
Three straight lines cut a regular yellow hexagon as shown, generating four green equilateral triangles of equal size. What is the ration of green to yellow areas.
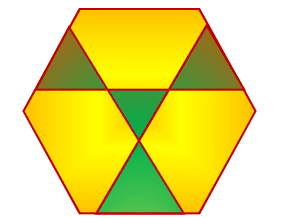
If the answer is in the form b a , where a and b are coprime positive integers, report a + b .
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
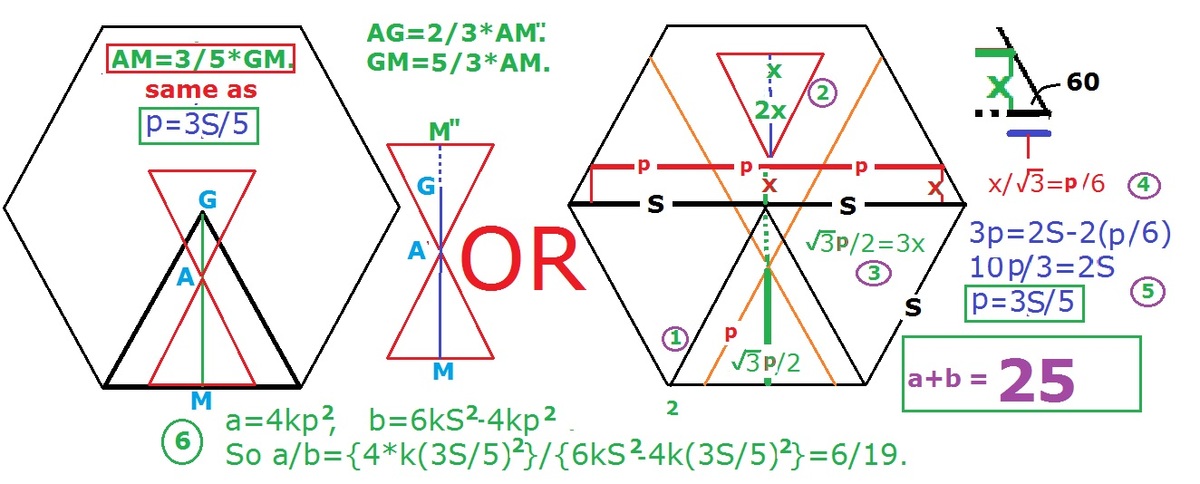
WLOG apothem of hexagon is 1. This is also the median of the six forming triangles.
The median of the six triangle forming the hexagonal can be clearly seen to be 1+2/3=5/3 times that of the four triangles.
Also the four and six triangles are similar equilateral triangles.
Thus the ratio of Green to Yellow areas=
6
∗
1
2
−
4
∗
(
3
/
5
)
2
4
∗
(
3
/
5
)
2
=
6
−
3
6
/
2
5
3
6
/
2
5
=
1
5
0
−
3
6
3
6
=
6
/
1
9
=
a
/
b
.
S
o
a
+
b
=
6
+
1
9
=
2
5
.
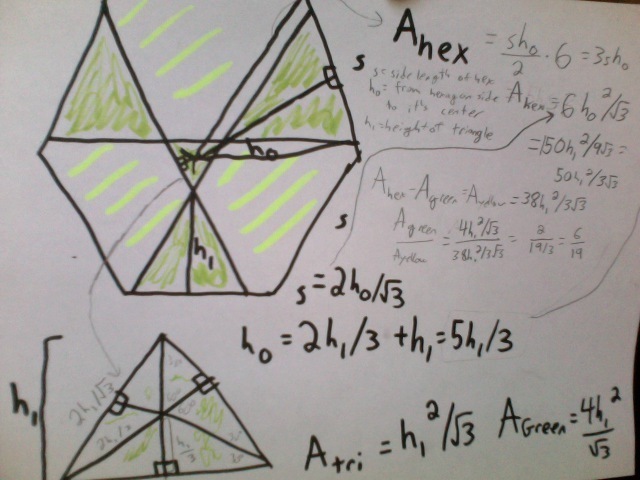

A h e x = 6 × 4 3 = 2 3 3
The height of △ A B O , which is O F = E F + O E = E F + 3 2 E F = 3 5 E F
The 3 2 comes in from the fact that O E is distance from the center of △ G H E to the vertex, and that is 3 2 of the median.
The sides of the green triangles are all 5 3 × A B = 5 3 , so the green area is
A 4 △ = 4 × 4 3 × ( 5 3 ) 2 = 2 5 9 3
Y E L L O W G R E E N = A h e x − A 4 △ A 4 △ = 2 3 3 − 2 5 9 3 2 5 9 3 = 2 5 − 6 6 = 1 9 6
Answer = 6 + 1 9 = 2 5