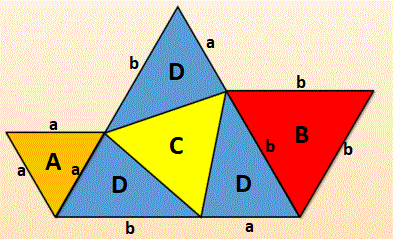
Four Equilateral triangles
There are four equilateral triangles shown in the figure. The number within each equilateral triangle represents its area.
What is the area of the yellow triangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution. When you came up with the 2k and 3k I was first like: darn he's making it unnecessary harder than needed, but it gives a nice result in which you don't need to calculate (which I did using 30-60-90 triangles and the same way of finding congruent triangles) a side, but come up with ratios.
Let the length of each side of orange △ be a , red △ be b and of the yellow △ be c . Then a 2 = 3 8 0 , b 2 = 3 1 8 0 , and c 2 = a 2 + b 2 − a b . So the area of the yellow △ is 2 0 + 4 5 − 4 3 3 × 8 0 × 1 8 0 = 6 5 − 3 0 = 3 5
The three blue triangles all have angles that are 6 0 ° , θ , and 1 2 0 ° − θ and one side congruent to the side of the yellow equilateral triangle, so they are all congruent by the ASA congruency theorem.
Let A and a be the area and side of the left equilateral triangle, B and b be the area and side of the right equilateral triangle, C be the area of the yellow equilateral triangle, D be the area of each of the blue triangles, and E be the area of the large equilateral triangle. The sides of E are then a + b , and E = C + 3 D .
By triangle area equations,
A = 4 3 a 2
B = 4 3 b 2
D = 2 1 a b sin 6 0 ° = 4 3 a b = A B
E = 4 3 ( a + b ) 2 = 4 3 a 2 + 2 4 3 a b + 4 3 b 2 = A + 2 D + B = A + B + 2 A B
C = E − 3 D = ( A + B + 2 A B ) − 3 A B = A + B − A B
In this question, A = 2 0 and B = 4 5 , so C = 2 0 + 4 5 − 2 0 ⋅ 4 5 = 3 5 .
Ditto, that was my approach too.
Next, let a and b be the side length of the triangles with areas 20 and 45 respectively. Then a 2 : b 2 = 2 0 : 4 5 = 4 : 9 , which implies that a : b = 2 : 3 . Let a = 2 k and b = 3 k . Let c be the side length of the yellow triangle.
As the 3 blue triangles are congruent, each of the triangles has side 2 k , 3 k , c and an angle 60 degree (as shown).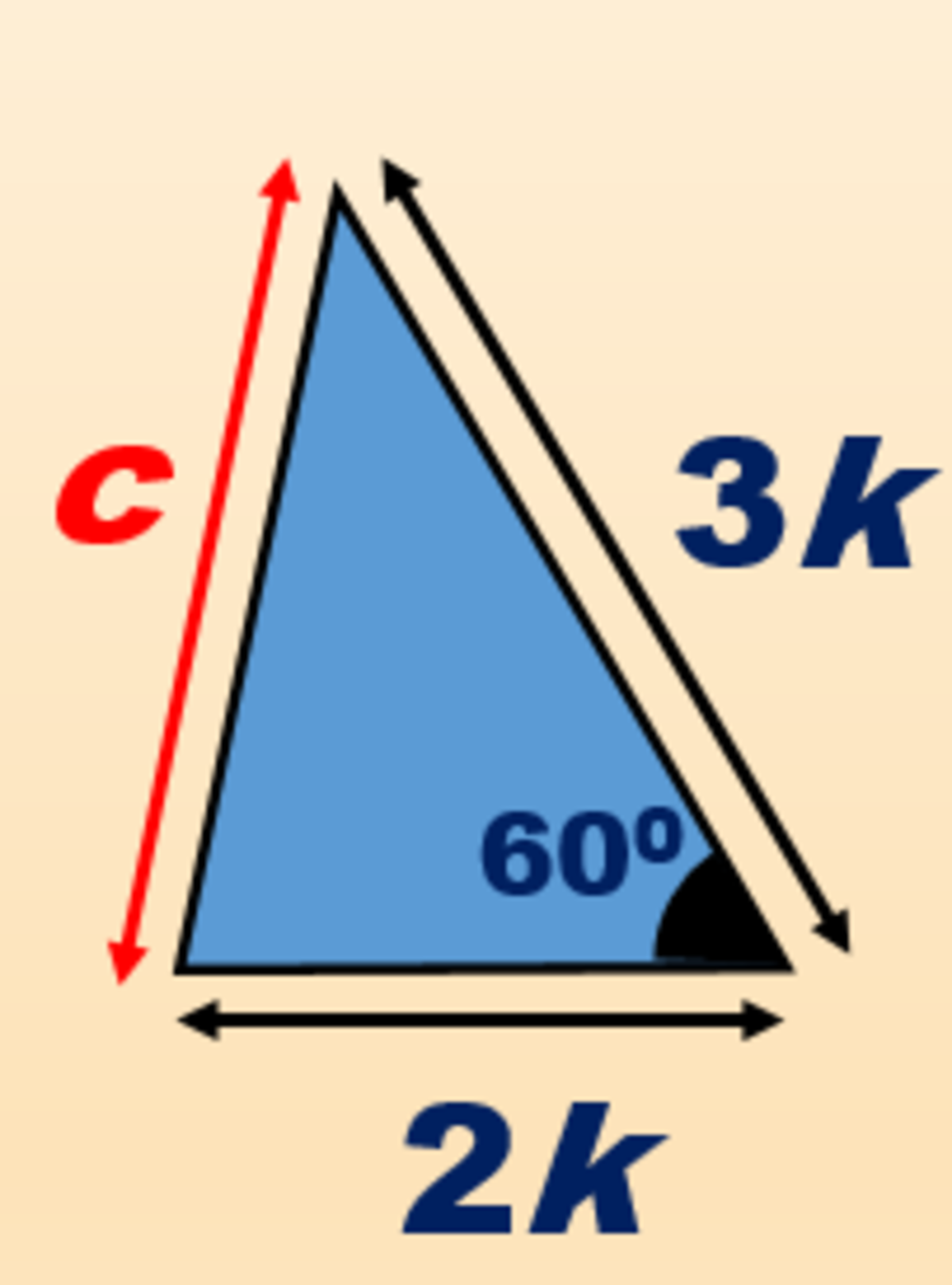
Using Cosine Rule, c 2 = a 2 + b 2 − 2 a b cos 6 0 ∘ = 7 k 2 .
Now a 2 : b 2 : c 2 = 4 : 9 : 7 = 2 0 : 4 5 : 3 5 . So the area of the yellow triangle is 35.
Watch this video for the explanation.