Four Fools, One Pool
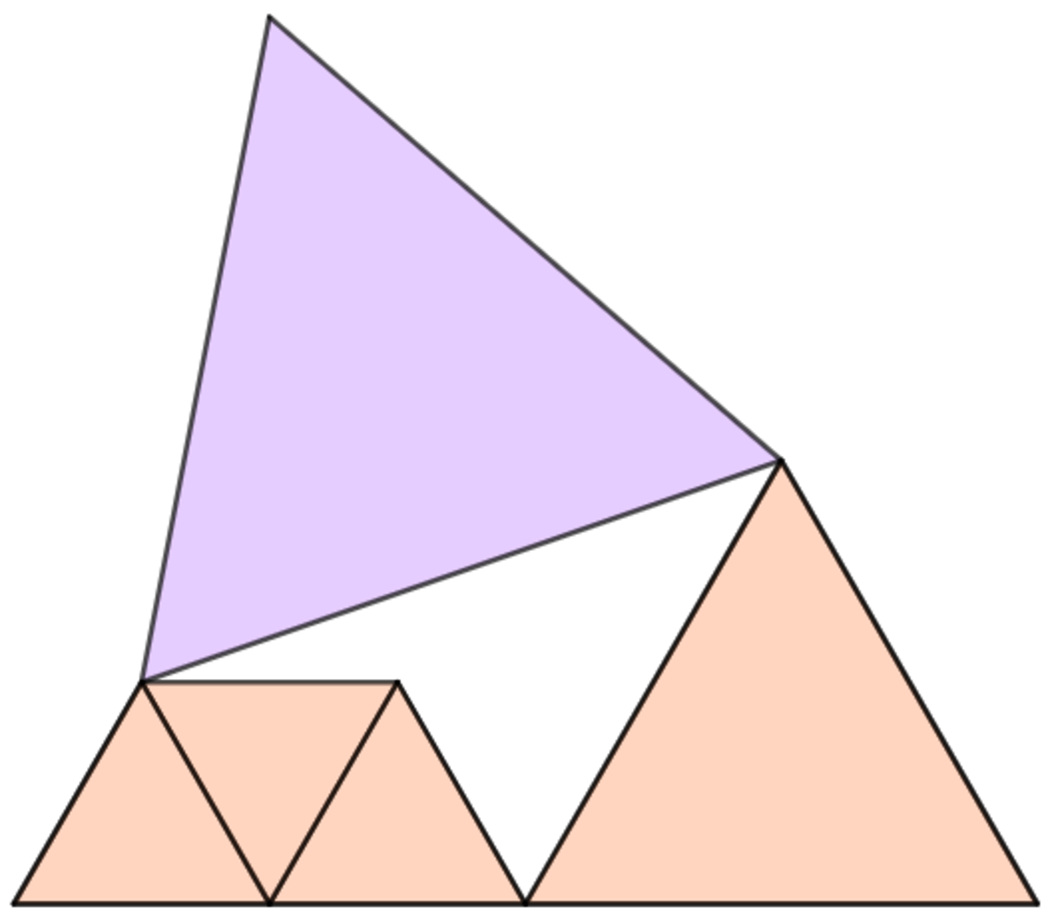
As shown above, four red equilateral triangles, where three of them are identical and tangential to each other, are positioned, such that the segments of three triangles are collinear. The large purple equilateral triangle that is not overlapping shares two points of tangency.
If Red is the area sum of all four equilateral triangles and Purple is the area of the purple triangle, which of the following must be true?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
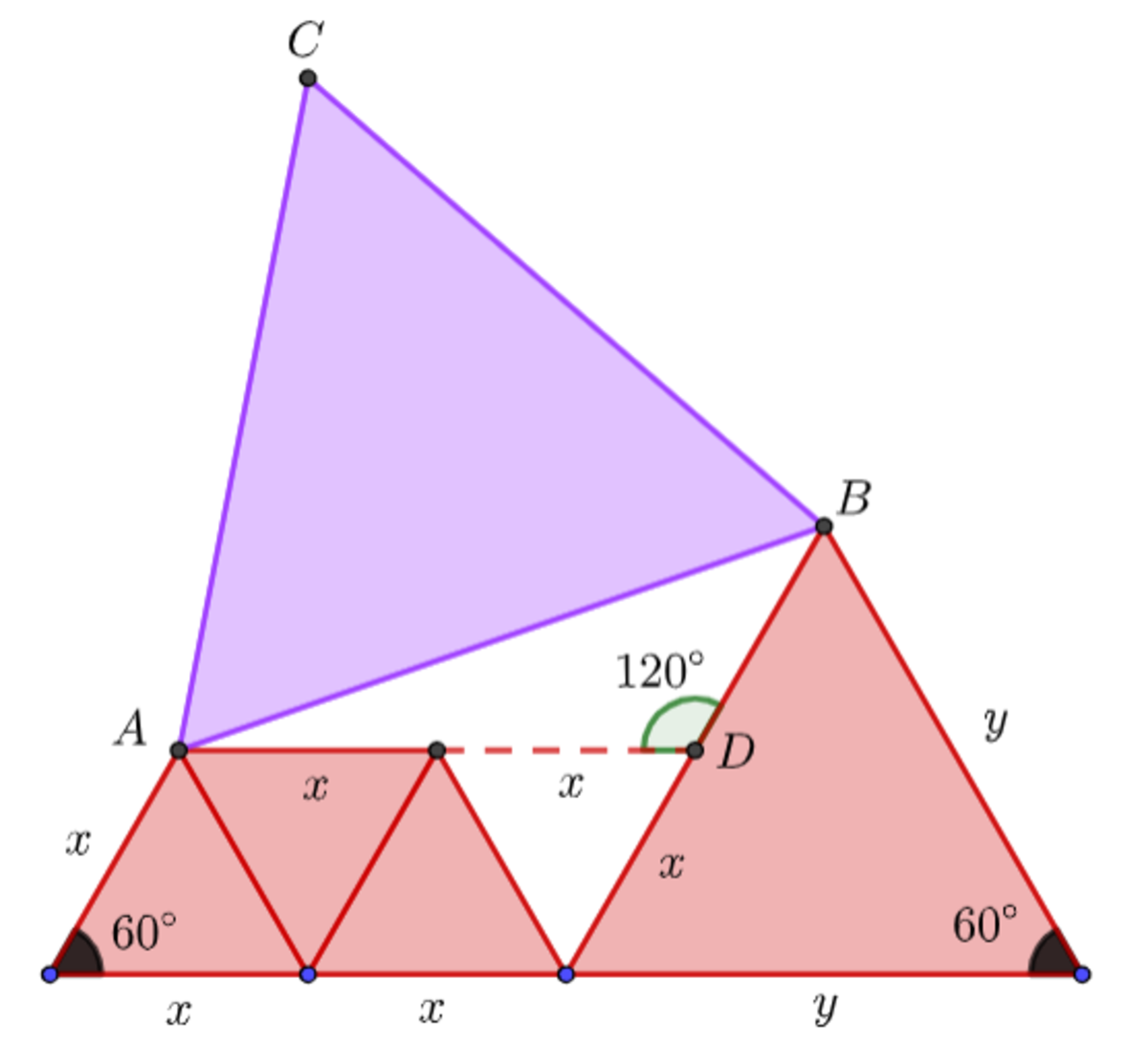 Applying the
Law of Cosines
, in
△
A
D
B
,
A
B
2
=
A
D
2
+
B
D
2
−
2
⋅
A
D
⋅
B
D
⋅
cos
∠
A
D
B
=
(
2
x
)
2
+
(
y
−
x
)
2
−
2
⋅
(
2
x
)
⋅
(
y
−
x
)
⋅
cos
1
2
0
∘
=
4
x
2
+
y
2
+
x
2
−
2
x
y
+
2
x
y
−
2
x
2
=
3
x
2
+
y
2
Therefore,
Red
Purple
∴
=
3
⋅
4
x
2
3
+
4
y
2
3
=
(
3
x
2
+
y
2
)
⋅
4
3
=
4
A
B
2
3
=
(
3
x
2
+
y
2
)
⋅
4
3
Red
=
Purple
Applying the
Law of Cosines
, in
△
A
D
B
,
A
B
2
=
A
D
2
+
B
D
2
−
2
⋅
A
D
⋅
B
D
⋅
cos
∠
A
D
B
=
(
2
x
)
2
+
(
y
−
x
)
2
−
2
⋅
(
2
x
)
⋅
(
y
−
x
)
⋅
cos
1
2
0
∘
=
4
x
2
+
y
2
+
x
2
−
2
x
y
+
2
x
y
−
2
x
2
=
3
x
2
+
y
2
Therefore,
Red
Purple
∴
=
3
⋅
4
x
2
3
+
4
y
2
3
=
(
3
x
2
+
y
2
)
⋅
4
3
=
4
A
B
2
3
=
(
3
x
2
+
y
2
)
⋅
4
3
Red
=
Purple
The straight line between the apex / summit of the leftmost little red equilateral triangle and the shared point of two red equilateral triangle of different sizes are perpendicular to the left slope side of big red equilateral triangle, so the two lines would be two legs of a right triangle and the purple's side would be the hypothenuse, no matter the size of the two biggest triangles' side length. Since the problem is asking about area, the smallest three can be rearranged into a bigger equilateral triangle by halving them and reconstructed with the new side being twice the height of the original.
Let the sides be p, q and r with q < r < p, and after reconstruction, 3 equilateral triangles combined into a bigger one with sides Q.
Q = √3 × q
The right triangle / Pythagorean equation would be
p² = r² + Q²
Multiply each term with 0.5(sin 60°)
(1/2)p²(sin 60°) = (1/2)r²(sin 60°) + (1/2)Q²(sin 60°)
(1/2)p²(sin 60°) = (1/2)r²(sin 60°) + (1/2)(3q²)(sin 60°)
= (1/2)r²(sin 60°) + (3) × (1/2)(q²)(sin 60°)
Area of big purple = Area of big red + Area of 3 small reds
Purple = Red
The equality hold for r ≤ q too as long as the overlapping area is accounted for both red and purple or none at all.