Four Kissing Circles
What is the radius of the small, red circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
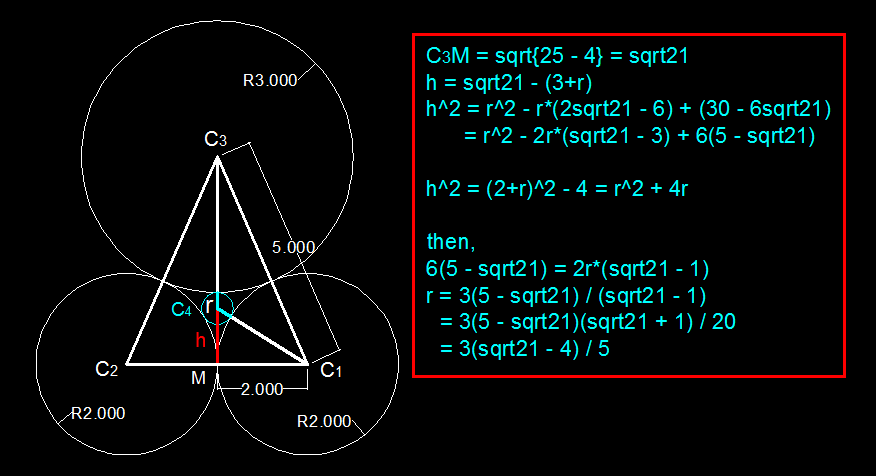
hello, can please write the solution using the decartes theorem
By Descarte's Circle Theorem,
To get the curvature of the three circles, just get the reciprocal of their radii. Those shall be your k 1, k 2, and k_3.
k_4=(1/2)+(1/2)+(1/3)+2sqrt[(1/2 * 1/2) + (1/2 * 1/3) + (1/2 * 1/3)]
k_4=4/3 + 2sqrt[(1/4) + (1/6) + (1/6)]
k_4=4/3 + 2sqrt(7/12)
k_4=4/3 + sqrt(21)/3
k_4=[4+sqrt(21)]/3
Note that since the circle is externally tangent to the three larger circles, its curvature is positive.
[4+sqrt(21)]/3=1/r
r=3/[4+sqrt(21)]
Rationalize the denominator,
r={3[4-sqrt(21)]}/(-5)
r=[12-3sqrt(21)]/(-5)
r=[3sqrt(21)-12]/5
r={3[sqrt(21)-4]}/5
how did you get from 4/3 + 2sqrt(7/12) to 4/3 +sqrt(21)/3 ?
Log in to reply
To get rid of the fraction under the radical, multiply 7/12 by 3/3. This results in a perfect square in the denominator that can be removed from the radical.
4/3 + 2√(7/12) = 4/3 + 2√(21/36) = 4/3 + (2√21)/6 = 4/3 +3√21
Log in to reply
Sorry, messed up the last term:
4/3 + 2√(7/12) = 4/3 + 2√(21/36) = 4/3 + (2√21)/6 = 4/3 +√(21)/3
A direct application of Descartes' Circle Theorem
r 4 1 r 4 1 r 4 r 4 = r 1 1 + r 2 1 + r 3 1 ± 2 r 1 r 2 1 + r 2 r 3 1 + r 3 r 1 1 = 2 1 + 2 1 + 3 1 ± 2 ( 2 ) ( 2 ) 1 + ( 2 ) ( 3 ) 1 + ( 3 ) ( 2 ) 1 = 3 4 + 2 1 2 7 = 3 4 + 3 7 = 3 4 + 2 1 = 2 1 + 4 3 = 5 3 ( 2 1 − 4 )