Four More Circles in a Box
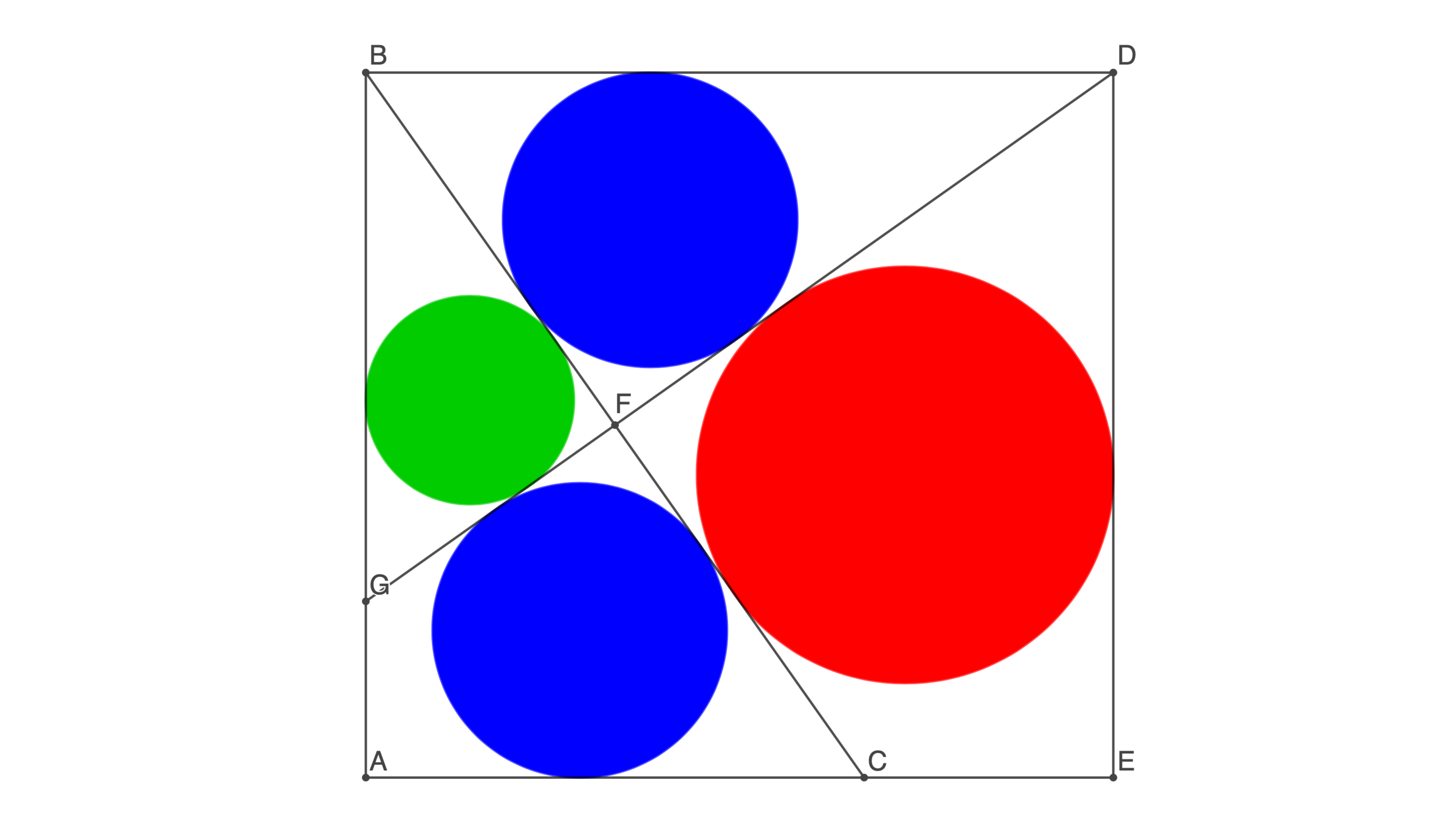
In rectangle A B D E , perpendicular segments B C and G D are drawn in such a way that four incircles can be drawn. If the blue incircles are congruent and the radius of the red incircle is twice the radius of the green incircle, what is the ratio A B B D ? If it can be expressed as c a b , where a , b , c are positive integers with b square-free and a , c coprime, submit a + b + c .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Extend G D and A E to meet at H , and extend B C and D E to meet at I , and label the diagram as follows:
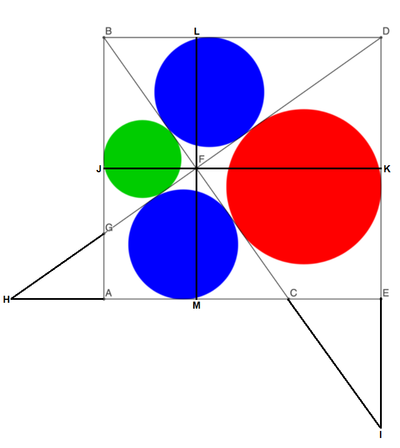
By alternate interior angles and vertical angles, △ F H C ∼ △ F D B by AA similarity, and since their incircles are congruent, △ F H C ≅ △ F D B , and L F = F M .
Likewise, △ F B G ∼ △ F I D by AA similarity, and since the radius of the red circle is twice the radius of the green circle, F K = 2 ⋅ J F , which means L D = 2 ⋅ B L .
△ L F B ∼ △ L D F by AA similarity, so L F B L = L D L F , or L F B L = 2 ⋅ B L L F , which solves to L F = 2 ⋅ B L .
Therefore, the ratio A B B D = 2 ⋅ L F B L + L D = 2 ⋅ 2 ⋅ B L B L + 2 ⋅ B L = 2 2 3 = 4 3 2 , so that a = 3 , b = 2 , c = 4 , and a + b + c = 9 .
Triangles △ F B D and △ F C H are similar, but since their ratio of similarity equals the ratio of their inradii, which is 1, in fact they are congruent and so are their altitudes to the hypotenuse, i.e. F K = F L = 2 q Likewise, △ F B G ∼ △ F J D , thus
F N F M = radius of red circle radius of green circle = 2 1 ⇒ F M = 3 p and F N = 3 2 p On right triangle △ F B D ,
F K 2 = K B ⋅ K D ⇒ F K 2 = F M ⋅ F N ⇒ ( 2 q ) 2 = 3 p ⋅ 3 2 p ⇒ q 2 p 2 = 8 9 ⇒ q p = 2 2 3 = 4 3 2 Hence, a + b + c = 3 + 2 + 4 = 9 .