Four More Incircles

Geometry Level 5

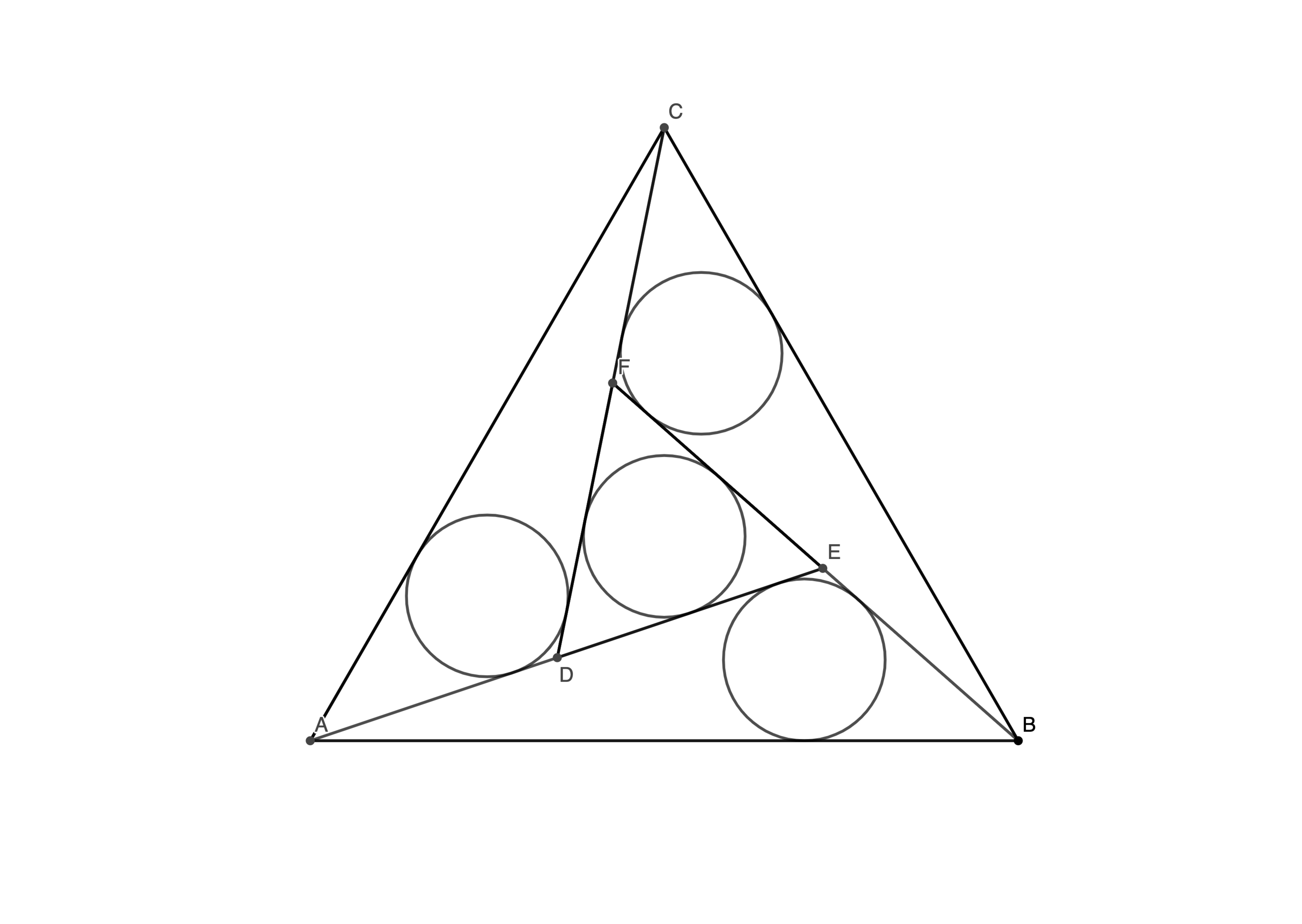
△ A B C \triangle ABC is the unit equilateral triangle. △ D E F \triangle DEF is an equilateral triangle. The four incircles are congruent. What is their radius? Express it as a − b c \sqrt \dfrac{a - \sqrt b}{c} , where b b is square-free, and submit a + b + c a+b+c

inspiritaion


The answer is 58.

Fletcher Mattox by Fletcher Mattox , 72, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

David Vreken
Feb 17, 2021

Extend C D CD to meet A B AB at G G , A E AE to meet B C BC at H H , B F BF to meet A C AC at I I , and let k = A G = B H k = AG = BH .

By the law of cosines on △ A B H \triangle ABH , A H = B H 2 + A B 2 − 2 ⋅ B H ⋅ A B ⋅ cos ⁡ ∠ A B H = k 2 + 1 − 2 ⋅ k ⋅ 1 2 = k 2 − k + 1 AH = \sqrt{BH^2 + AB^2 - 2 \cdot BH \cdot AB \cdot \cos \angle ABH} = \sqrt{k^2 + 1 - 2 \cdot k \cdot \frac{1}{2}} = \sqrt{k^2 - k + 1} .

Since △ A G D ∼ △ B H E \triangle AGD \sim \triangle BHE by AA similarity, A D = A G ⋅ A B A H = k ⋅ 1 k 2 − k + 1 = k k 2 − k + 1 = E B AD = AG \cdot \cfrac{AB}{AH} = k \cdot \cfrac{1}{\sqrt{k^2 - k + 1}} = \cfrac{k}{\sqrt{k^2 - k + 1}} = EB .

Also, G D = A F ⋅ B H A H = k ⋅ k k 2 − k + 1 = k 2 k 2 − k + 1 = E H GD = AF \cdot \cfrac{BH}{AH} = k \cdot \cfrac{k}{\sqrt{k^2 - k + 1}} = \cfrac{k^2}{\sqrt{k^2 - k + 1}} = EH .

Then D E = A H − A D − E H = k 2 − k + 1 − k k 2 − k + 1 − k 2 k 2 − k + 1 = 1 − 2 k k 2 − k + 1 DE = AH - AD - EH = \sqrt{k^2 - k + 1} - \cfrac{k}{\sqrt{k^2 - k + 1}} - \cfrac{k^2}{\sqrt{k^2 - k + 1}} = \cfrac{1 - 2k}{\sqrt{k^2 - k + 1}} .

And A E = A D + D E = k k 2 − k + 1 + 1 − 2 k k 2 − k + 1 = 1 − k k 2 − k + 1 AE = AD + DE = \cfrac{k}{\sqrt{k^2 - k + 1}} + \cfrac{1 - 2k}{\sqrt{k^2 - k + 1}} = \cfrac{1 - k}{\sqrt{k^2 - k + 1}} .

As an incircle of equilateral △ D E F \triangle DEF , r = 1 2 3 ⋅ D E = 1 2 3 ⋅ 1 − 2 k k 2 − k + 1 = 1 − 2 k 2 3 k 2 − k + 1 r = \cfrac{1}{2\sqrt{3}} \cdot DE = \cfrac{1}{2\sqrt{3}} \cdot \cfrac{1 - 2k}{\sqrt{k^2 - k + 1}} = \cfrac{1 - 2k}{2\sqrt{3}\sqrt{k^2 - k + 1}} .

As an incircle of △ A E B \triangle AEB , r = A E ⋅ E B ⋅ sin ⁡ ∠ A E B A E + E B + A B = 1 − k k 2 − k + 1 ⋅ k k 2 − k + 1 ⋅ 3 2 1 − k k 2 − k + 1 + k k 2 − k + 1 + 1 = 3 2 3 k 2 − k + 1 − 3 2 r = \cfrac{AE \cdot EB \cdot \sin \angle AEB}{AE + EB + AB} = \cfrac{\frac{1 - k}{\sqrt{k^2 - k + 1}} \cdot \frac{k}{\sqrt{k^2 - k + 1}} \cdot \frac{\sqrt{3}}{2}}{\frac{1 - k}{\sqrt{k^2 - k + 1}} + \frac{k}{\sqrt{k^2 - k + 1}} + 1} = \cfrac{3}{2\sqrt{3}\sqrt{k^2 - k + 1}} - \cfrac{\sqrt{3}}{2} .

So r = 1 − 2 k 2 3 k 2 − k + 1 = 3 2 3 k 2 − k + 1 − 3 2 r = \cfrac{1 - 2k}{2\sqrt{3}\sqrt{k^2 - k + 1}} = \cfrac{3}{2\sqrt{3}\sqrt{k^2 - k + 1}} - \cfrac{\sqrt{3}}{2} , which solves to k = 17 − 3 21 10 k = \cfrac{17 - 3\sqrt{21}}{10} and r = 5 − 21 32 r = \sqrt{\cfrac{5 - \sqrt{21}}{32}} .

Therefore, a = 5 a = 5 , b = 21 b = 21 , c = 32 c = 32 , and a + b + c = 58 a + b + c = \boxed{58} .

3 Helpful 2 Interesting 4 Brilliant 0 Confused

Nice - once again quite a different approach to mine. It's interesting how close the values of A D AD and D E DE are.

By the way, the answer can also be written as 7 − 3 8 \frac{\sqrt7-\sqrt3}{8}

Chris Lewis - 3 months, 3 weeks ago

Hi David, I always appreciate your solutions, which are amongst my favorites. Thanks so much. I have a question here : I do not understand the end of the first line. I would have expected √(k^2-k+1) instead of √(k^2-2k+1) as we have 2.k.(1/2).

Gerard Boileau - 3 months, 2 weeks ago

Log in to reply

Thanks, it should have been k 2 − k + 1 \sqrt{k^2 - k + 1} . It was a typo that I kept copying and pasting in the rest of the problem. It should be fixed now.

David Vreken - 3 months, 2 weeks ago

Thanks ! It's always a pleasure to see how you solve this kind of problem almost without trigonometry !

Gerard Boileau - 3 months, 2 weeks ago

Hi David, I fell really stupid but I cannot find out how to simplify the equation of ∆AEB incircle radius, to get r= 3/(2√3√(k^2-k+1) -√3/2. Would you be kind enough to give some intermediate results or tell "the trick" ? Thanks a lot.

Gerard Boileau - 3 months, 2 weeks ago

Log in to reply

If you start by multiplying the expression by k 2 − k + 1 k 2 − k + 1 \cfrac{\sqrt{k^2 - k + 1}}{\sqrt{k^2 - k + 1}} , then:

r = 1 − k k 2 − k + 1 ⋅ k k 2 − k + 1 ⋅ 3 2 1 − k k 2 − k + 1 + k k 2 − k + 1 + 1 ⋅ k 2 − k + 1 k 2 − k + 1 = ( 1 − k ) k k 2 − k + 1 ⋅ 3 2 1 + k 2 − k + 1 r = \cfrac{\frac{1 - k}{\sqrt{k^2 - k + 1}} \cdot \frac{k}{\sqrt{k^2 - k + 1}} \cdot \frac{\sqrt{3}}{2}}{\frac{1 - k}{\sqrt{k^2 - k + 1}} + \frac{k}{\sqrt{k^2 - k + 1}} + 1} \cdot \cfrac{\sqrt{k^2 - k + 1}}{\sqrt{k^2 - k + 1}} = \cfrac{\frac{(1 - k)k}{\sqrt{k^2 - k + 1}} \cdot \frac{\sqrt{3}}{2}}{1 + \sqrt{k^2 - k + 1}}

Then multiply the expression by 1 − k 2 − k + 1 1 − k 2 − k + 1 \cfrac{1 - \sqrt{k^2 - k + 1}}{1 - \sqrt{k^2 - k + 1}} , so:

r = ( 1 − k ) k k 2 − k + 1 ⋅ 3 2 ⋅ ( 1 − k 2 − k + 1 ) ( 1 + k 2 − k + 1 ) ( 1 − k 2 − k + 1 ) = ( 1 − k ) k k 2 − k + 1 ⋅ 3 2 ⋅ ( 1 − k 2 − k + 1 ) ( 1 − k ) k r = \cfrac{\frac{(1 - k)k}{\sqrt{k^2 - k + 1}} \cdot \frac{\sqrt{3}}{2} \cdot (1 - \sqrt{k^2 - k + 1})}{(1 + \sqrt{k^2 - k + 1})(1 - \sqrt{k^2 - k + 1})} = \cfrac{\frac{(1 - k)k}{\sqrt{k^2 - k + 1}} \cdot \frac{\sqrt{3}}{2} \cdot (1 - \sqrt{k^2 - k + 1})}{(1 - k)k}

Then simplifying:

r = ( 1 − k ) k k 2 − k + 1 ⋅ 3 2 ⋅ ( 1 − k 2 − k + 1 ) ( 1 − k ) k = 1 k 2 − k + 1 ⋅ 3 2 ⋅ ( 1 − k 2 − k + 1 ) = 3 2 3 k 2 − k + 1 − 3 2 r = \cfrac{\frac{(1 - k)k}{\sqrt{k^2 - k + 1}} \cdot \frac{\sqrt{3}}{2} \cdot (1 - \sqrt{k^2 - k + 1})}{(1 - k)k} = \cfrac{1}{\sqrt{k^2 - k + 1}} \cdot \cfrac{\sqrt{3}}{2} \cdot (1 - \sqrt{k^2 - k + 1}) = \cfrac{3}{2\sqrt{3}\sqrt{k^2 - k + 1}} - \cfrac{\sqrt{3}}{2} .

David Vreken - 3 months, 2 weeks ago

thank you so much ! I really do appreciate your help and how much I can learn from your elegant solutions ! Gerard.

Gerard Boileau - 3 months, 2 weeks ago

Log in to reply

You're very welcome!

David Vreken - 3 months, 2 weeks ago
Chew-Seong Cheong
Feb 18, 2021

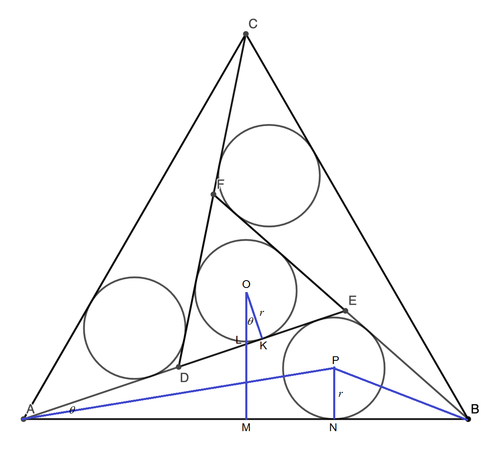
Let the centers of the middle and the right circles be O O and P P respectively, O M OM and P N PN be perpendicular to A B AB , O K OK be perpendicular to A E AE , and O M OM and A E AE intersect at L L . Let ∠ E A B = ∠ L O K = θ \angle EAB = \angle LOK = \theta , then ∠ E B A = 6 0 ∘ − θ \angle EBA = 60^\circ - \theta , and the radius of the four congruent circles be r r .

Then we have:

A N + N B = A B r cot ⁡ θ 2 + r cot ⁡ ( 3 0 ∘ − θ 2 ) = 1 Let t = tan ⁡ θ 2 r t + 3 + t 1 − 3 t ⋅ r = 1 ⟹ r = t ( 1 − 3 t ) 1 + t 2 \begin{aligned} AN + NB & = AB \\ r \cot \frac \theta 2 + r \cot \left(30^\circ - \frac \theta 2\right) & = 1 & \small \blue{\text{Let }t = \tan \frac \theta 2} \\ \frac rt + \frac {\sqrt 3 + t}{1-\sqrt 3t} \cdot r & = 1 \\ \implies r & = \frac {t(1-\sqrt 3t)}{1+t^2} \end{aligned}

Note that O O is also the centroid of △ A B C \triangle ABC . Therefore O M = 3 6 OM = \frac {\sqrt 3}6 . Then

O L + L M = O M r sec ⁡ θ + 1 2 tan ⁡ θ = 3 6 1 + t 2 1 − t 2 ⋅ r + t 1 − t 2 = 3 6 ⟹ r = 3 − 6 t − 3 t 2 6 ( 1 + t 2 ) \begin{aligned} OL + LM & = OM \\ r \sec \theta + \frac 12 \tan \theta & = \frac {\sqrt 3}6 \\ \frac {1+t^2}{1-t^2} \cdot r + \frac t{1-t^2} & = \frac {\sqrt 3}6 \\ \implies r & = \frac {\sqrt 3 - 6t - \sqrt 3 t^2}{6(1+t^2)} \end{aligned}

Therefore

3 − 6 t − 3 t 2 6 ( 1 + t 2 ) = t ( 1 − 3 t ) 1 + t 2 5 3 t 2 − 12 t + 3 = 0 ⟹ t = 6 − 21 5 3 = 2 3 − 7 5 \begin{aligned} \frac {\sqrt 3 - 6t - \sqrt 3 t^2}{6(1+t^2)} & = \frac {t(1-\sqrt 3t)}{1+t^2} \\ 5\sqrt 3 t^2 - 12 t + \sqrt 3 & = 0 \\ \implies t & = \frac {6-\sqrt{21}}{5\sqrt 3} = \frac {2\sqrt 3 - \sqrt 7}5 \end{aligned}

Then r = t ( 1 − 3 t ) 1 + t 2 = 5 − 21 32 r = \dfrac {t(1-\sqrt 3t)}{1+t^2} = \sqrt{\dfrac {5-\sqrt{21}}{32}} . Therefore a + b + c = 58 a+b+c = \boxed{58} .

3 Helpful 2 Interesting 3 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...